Difference between revisions of "Logarithmic integral"
From specialfunctionswiki
| (4 intermediate revisions by the same user not shown) | |||
| Line 17: | Line 17: | ||
[[Prime counting function]] <br /> | [[Prime counting function]] <br /> | ||
| − | + | =References= | |
| + | * {{PaperReference|On certain definite integrals involving the exponential-integral|1881|James Whitbread Lee Glaisher|prev=Exponential integral Ei series|next=Relationship between logarithmic integral and exponential integral}} | ||
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Exponential integral Ei|next=Exponential integral E}}: $5.1.3$ | ||
| + | |||
| + | {{:Logarithm and friends footer}} | ||
| + | {{:*-integral functions footer}} | ||
| + | |||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 03:33, 17 March 2018
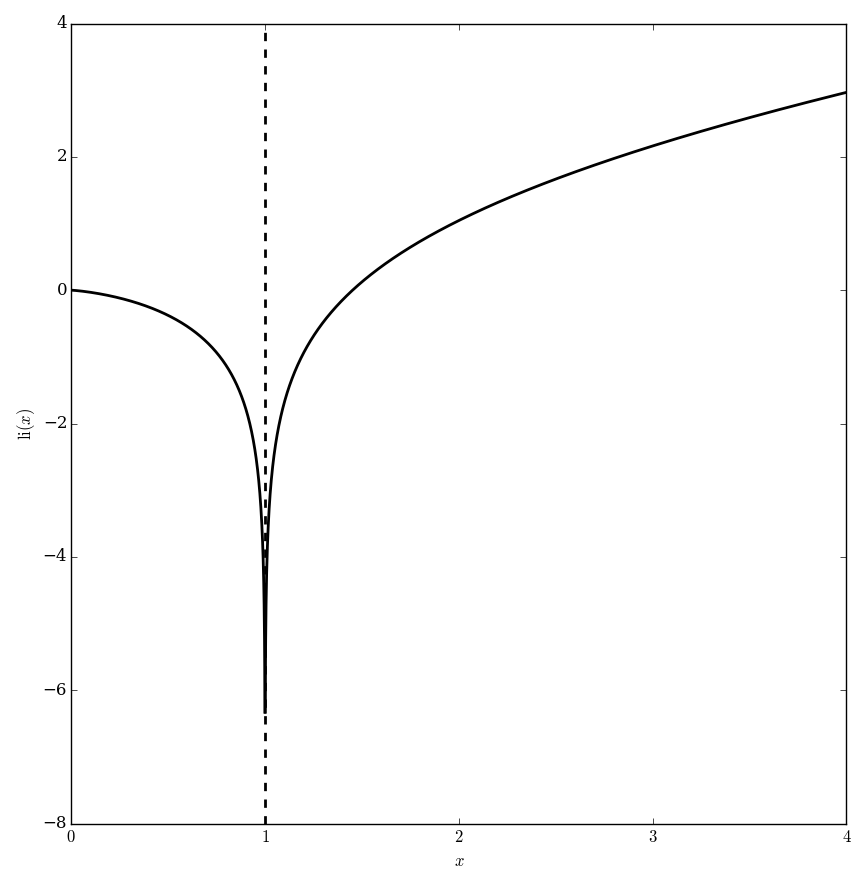
The logarithmic integral is $$\mathrm{li}(x) = \displaystyle\int_0^x \dfrac{1}{\log(t)} \mathrm{d}t,$$ where $\log$ denotes the logarithm.
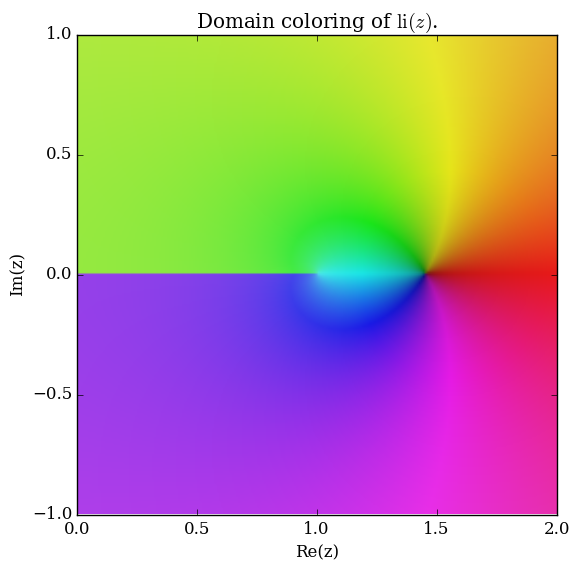
Domain coloring of $\mathrm{li}$.
Properties
Relationship between logarithmic integral and exponential integral
Prime number theorem, logarithmic integral
See Also
References
- James Whitbread Lee Glaisher: On certain definite integrals involving the exponential-integral (1881)... (previous)... (next)
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $5.1.3$