Latest revision as of 18:24, 16 June 2018

The Lambert $W$ function is the (multi-valued) function that satisfies the equation $$z=W(z)e^{W(z)}.$$

Properties

@@ Line 1: / Line 1: @@
-Let $z \in \mathbb{C}$ and define the Lambert $W$ function by the relation $z=W(z)e^{W(z)}$. This function has two branches.
+__NOTOC__
+The Lambert $W$ function is the (multi-valued) function that satisfies the equation
+$$z=W(z)e^{W(z)}.$$
+<div align="center">
+<gallery>
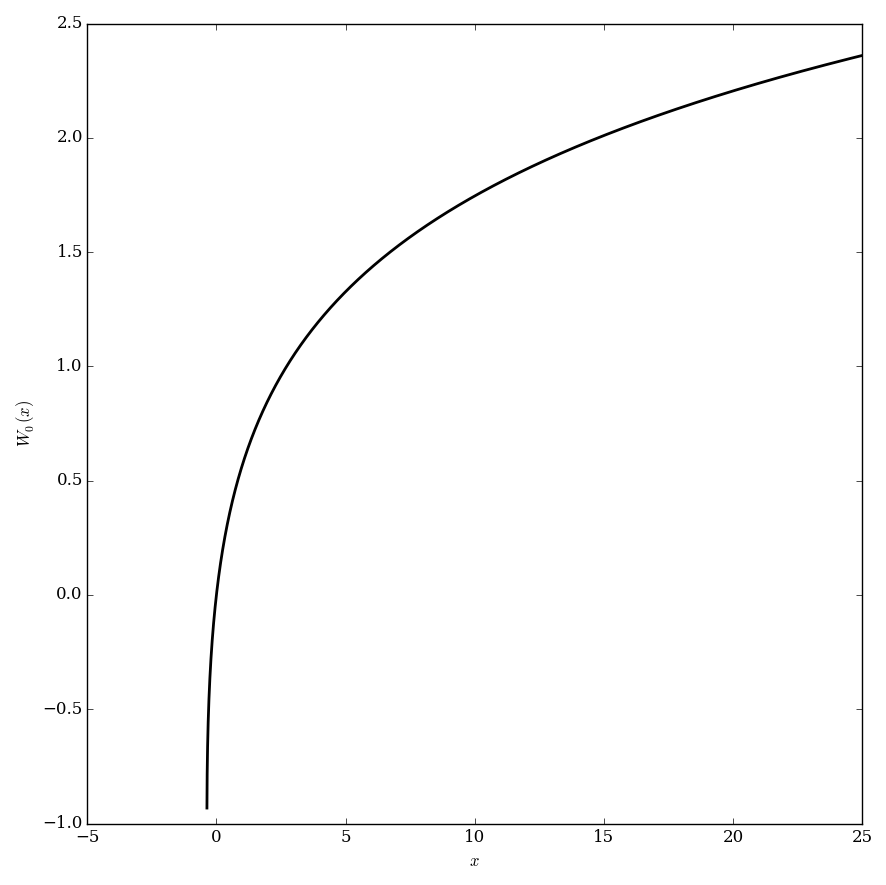
+File:Lambertw0plot.png|Plot of the principal branch $W_0$.
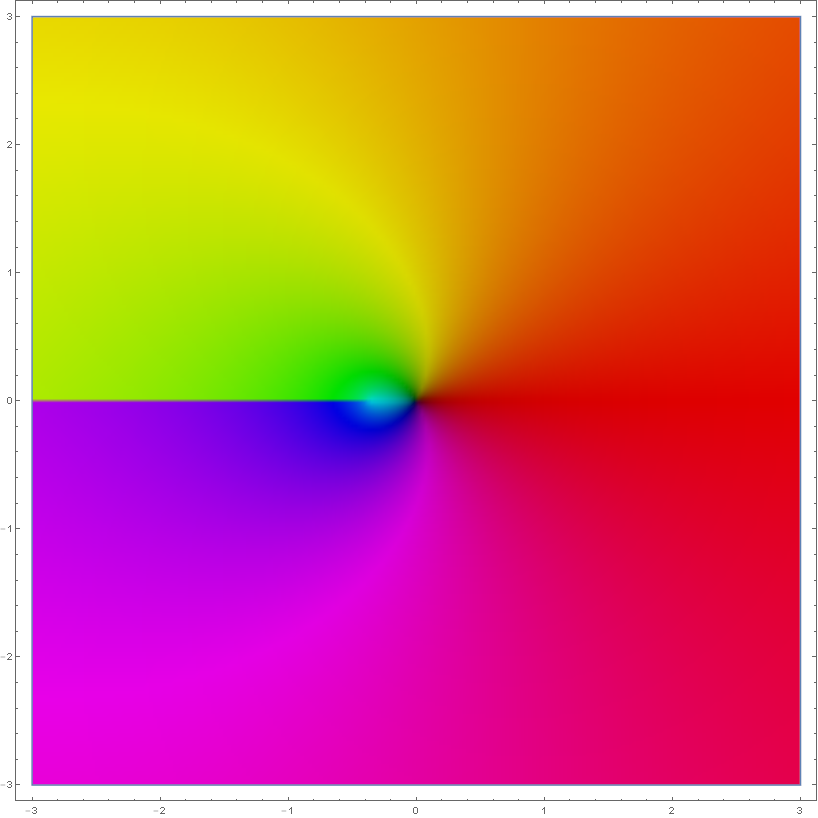
+File:Complexlambertw0.png|[[Domain coloring]] of [[analytic continuation]] of branch $W_0(x)$ to $\mathbb{C}$.
+File:Complexlambertw-1.png|[[Domain coloring]] of [[analytic continuation]] of branch $W_{-1}(x)$ to $\mathbb{C}$.
+</gallery>
+</div>
+=Properties=
+=Videos=
+*[https://www.youtube.com/watch?v=AJD8kh3DSAM 6: Recursion, Infinite Tetrations and the Lambert W Function (4 August 2014)]
+=External links=
+*[http://arxiv.org/pdf/1003.1628.pdf Having fun with the Lambert $W(x)$ function]
+=See also=
+[[Lambert W0]]<br />
+[[Lambert W1]]<br />
+=References=
+* {{PaperReference|On the Lambert W function|1996|R. M. Corless|author2=G. H. Gonnet|author3=D.E.G. Hare|author4=D.J. Jeffrey|author4=D.E. Knuth|prev=findme|next=findme}} $(1.5)$
+[[Category:SpecialFunction]]