Difference between revisions of "Clausen sine"
From specialfunctionswiki
(Created page with "Let $s \in \mathbb{C}$. The Clausen sine function $\mathrm{Cl}_s \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by the formula $$\mathrm{Cl}_s(z)=\displaystyle\sum_{k=1}...") |
|||
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Let $s \in \mathbb{C}$. The Clausen sine function $\mathrm{Cl}_s \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined | + | Let $s \in \mathbb{C}$. The Clausen sine function $\mathrm{Cl}_s \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined as the [[analytic continuation]] of the series |
$$\mathrm{Cl}_s(z)=\displaystyle\sum_{k=1}^{\infty} \dfrac{\sin(kz)}{k^s},$$ | $$\mathrm{Cl}_s(z)=\displaystyle\sum_{k=1}^{\infty} \dfrac{\sin(kz)}{k^s},$$ | ||
where $\sin$ denotes [[sine]]. | where $\sin$ denotes [[sine]]. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
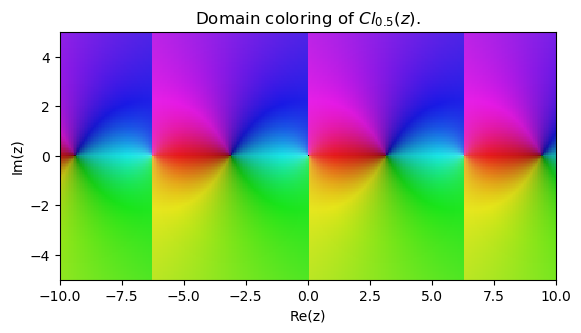
| + | File:Clausensine0.5.png|Graph of $\mathrm{Cl}_{0.5}$. | ||
| + | </gallery> | ||
| + | </div> | ||
=Properties= | =Properties= | ||
| + | |||
| + | =See also= | ||
| + | [[Clausen cosine]]<br /> | ||
=References= | =References= | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 19:44, 7 September 2020
Let $s \in \mathbb{C}$. The Clausen sine function $\mathrm{Cl}_s \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined as the analytic continuation of the series $$\mathrm{Cl}_s(z)=\displaystyle\sum_{k=1}^{\infty} \dfrac{\sin(kz)}{k^s},$$ where $\sin$ denotes sine.