Difference between revisions of "Q-Gamma"
(→References) |
|||
| (18 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Let $0<q<1$. Define | + | __NOTOC__ |
| − | $$\Gamma_q( | + | Let $0<q<1$. Define the $q$-gamma function by the formula |
| − | where $(\cdot;\cdot)_{\infty}$ denotes the [[q- | + | $$\Gamma_q(z) = \dfrac{(q;q)_{\infty}}{(q^z;q)_{\infty}}(1-q)^{1-z},$$ |
| + | where $(\cdot;\cdot)_{\infty}$ denotes the [[q-shifted factorial]]. The function $\Gamma_q$ is a [[q-analogue | $q$-analogue]] of the [[gamma function]]. | ||
| − | + | <div align="center"> | |
| + | <gallery> | ||
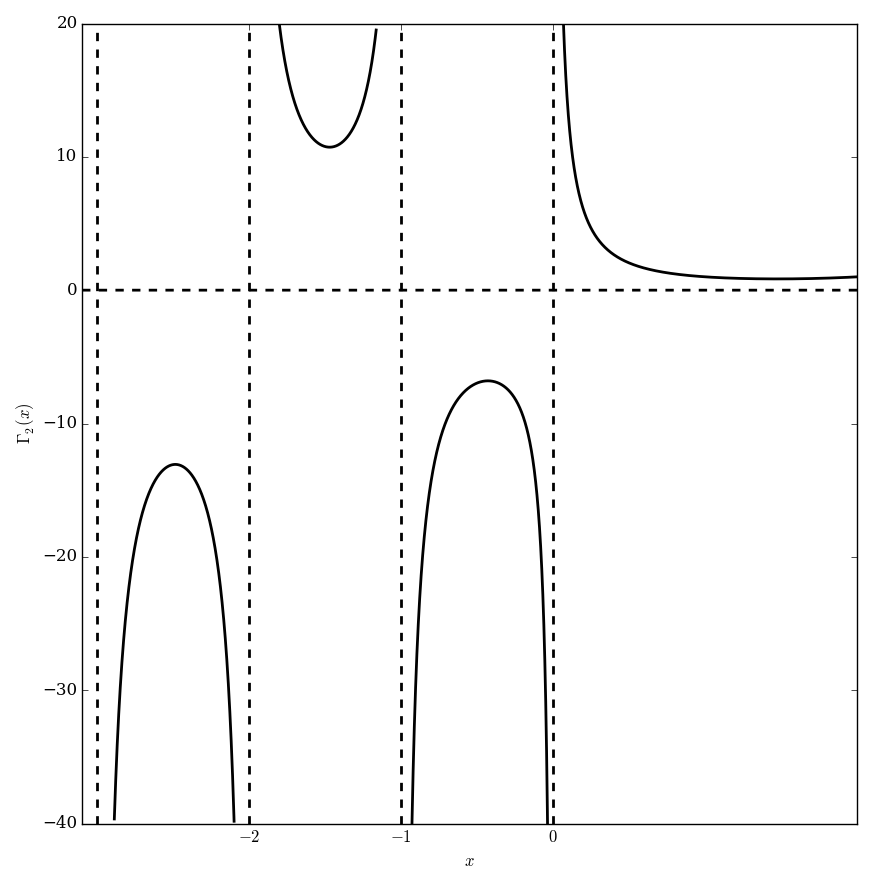
| + | File:Qgamma,q=2plot.png|Graph of $\Gamma_2$. | ||
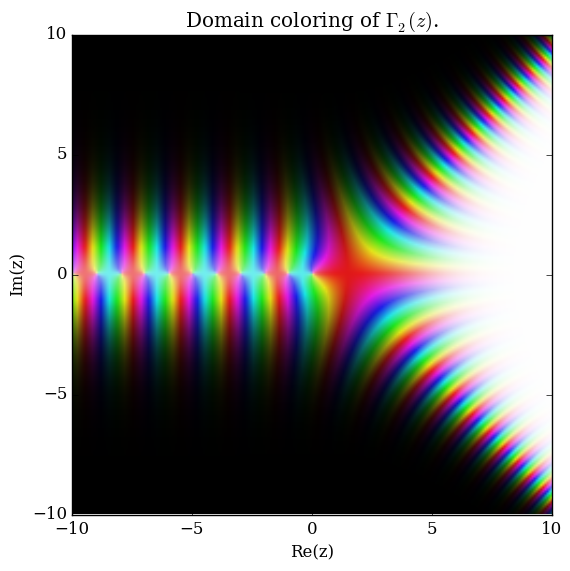
| + | File:Complexqgammaq=2plot.png|[[Domain coloring]] of $\Gamma_2$. | ||
| + | </gallery> | ||
| + | </div> | ||
=Properties= | =Properties= | ||
| − | + | [[q-Gamma at z+1]]<br /> | |
| − | + | [[q-Gamma at 1]]<br /> | |
| − | + | [[q-Gamma at 2]]<br /> | |
| − | |||
| − | |||
| − | </ | ||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
| − | + | <strong>Theorem ($q$-Bohr-Mollerup):</strong> Let $f$ be a function which satisfies | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <strong>Theorem ($q$- | ||
$$f(x+1) = \dfrac{1-q^x}{1-q}f(x)$$ | $$f(x+1) = \dfrac{1-q^x}{1-q}f(x)$$ | ||
for some $q \in (0,1)$, | for some $q \in (0,1)$, | ||
| Line 36: | Line 25: | ||
Then $f(x) = \Gamma_q(x)$. | Then $f(x) = \Gamma_q(x)$. | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| − | <strong>Proof:</strong> | + | <strong>Proof:</strong> █ |
</div> | </div> | ||
</div> | </div> | ||
| Line 44: | Line 33: | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
<strong>Proof:</strong> proof goes here █ | <strong>Proof:</strong> proof goes here █ | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | <div class="toccolours mw-collapsible mw-collapsed"> | ||
| + | <strong>Theorem:</strong> ([[q-analog|$q$-analog]]) The following formula holds: | ||
| + | $$\displaystyle\lim_{q \rightarrow 1^-} \Gamma_q(z) = \Gamma(z),$$ | ||
| + | where $\Gamma_q$ is the [[q-Gamma]] function and $\Gamma$ is the [[gamma]] function. | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <strong>Proof:</strong> █ | ||
</div> | </div> | ||
</div> | </div> | ||
=References= | =References= | ||
| − | + | * {{PaperReference|The q-Gamma and q-Beta functions|1978|Richard Askey|next=findme}} | |
| − | [ | + | * {{PaperReference|The q-gamma function for q greater than 1|1980|Daniel S. Moak|next=Q-shifted factorial}} |
| + | |||
| + | {{:q-calculus footer}} | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 00:13, 30 May 2017
Let $0<q<1$. Define the $q$-gamma function by the formula $$\Gamma_q(z) = \dfrac{(q;q)_{\infty}}{(q^z;q)_{\infty}}(1-q)^{1-z},$$ where $(\cdot;\cdot)_{\infty}$ denotes the q-shifted factorial. The function $\Gamma_q$ is a $q$-analogue of the gamma function.
Domain coloring of $\Gamma_2$.
Properties
q-Gamma at z+1
q-Gamma at 1
q-Gamma at 2
Theorem ($q$-Bohr-Mollerup): Let $f$ be a function which satisfies $$f(x+1) = \dfrac{1-q^x}{1-q}f(x)$$ for some $q \in (0,1)$, $$f(1)=1,$$ and $\log f(x)$ is convex for $x>0$. Then $f(x) = \Gamma_q(x)$.
Proof: █
Theorem (Legendre Duplication Formula): $\Gamma_q(2x)\Gamma_{q^2}\left(\dfrac{1}{2}\right)=\Gamma_{q^2}(x)\Gamma_{q^2}\left( x +\dfrac{1}{2} \right)(1+q)^{2x+1}$
Proof: proof goes here █
Theorem: ($q$-analog) The following formula holds: $$\displaystyle\lim_{q \rightarrow 1^-} \Gamma_q(z) = \Gamma(z),$$ where $\Gamma_q$ is the q-Gamma function and $\Gamma$ is the gamma function.
Proof: █
References
- Richard Askey: The q-Gamma and q-Beta functions (1978)... (next)
- Daniel S. Moak: The q-gamma function for q greater than 1 (1980)... (next)