Difference between revisions of "Reciprocal gamma"
From specialfunctionswiki
(Created page with "The reciprocal gamma function is the homomorphic function $\dfrac{1}{\Gamma(z)}$, where $\Gamma$ denotes the gamma function. 500px") |
|||
| (17 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The reciprocal gamma function is | + | The reciprocal gamma function $\dfrac{1}{\Gamma}$ is defined by |
| + | $$\left( \dfrac{1}{\Gamma} \right)(z) =\dfrac{1}{\Gamma(z)},$$ | ||
| + | where $\Gamma$ denotes the [[gamma function]]. | ||
| − | [[File: | + | <div align="center"> |
| + | <gallery> | ||
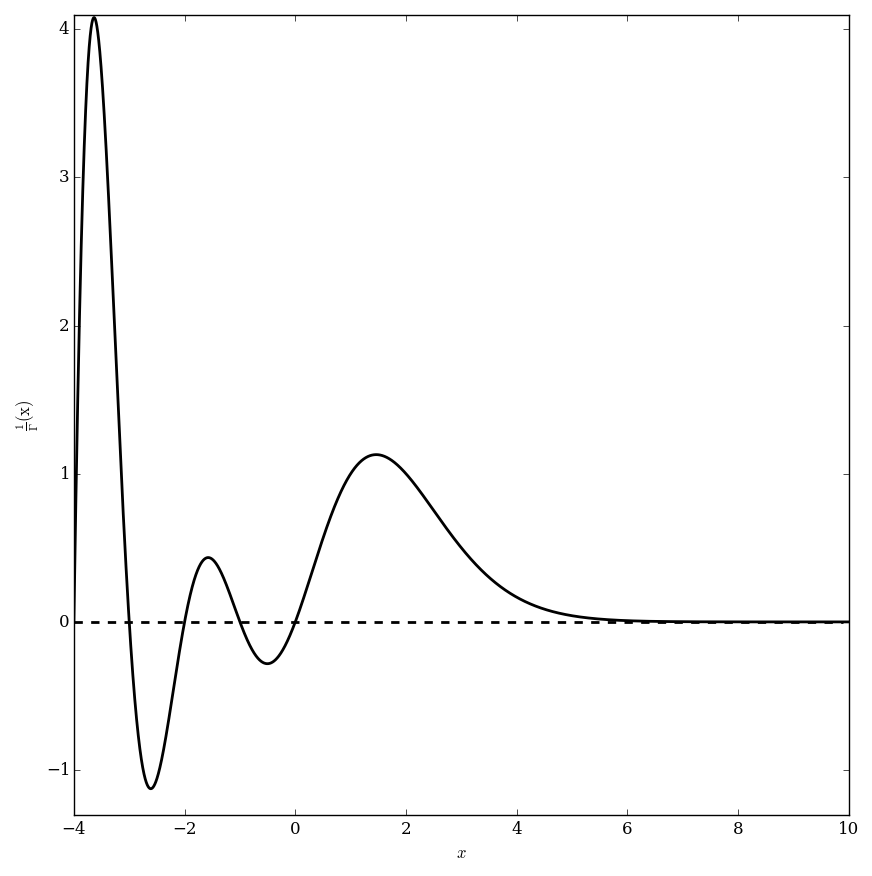
| + | File:Reciprocalgammaplotonneg4to10.png|Graph of $\dfrac{1}{\Gamma}$ on $[-4,10]$. | ||
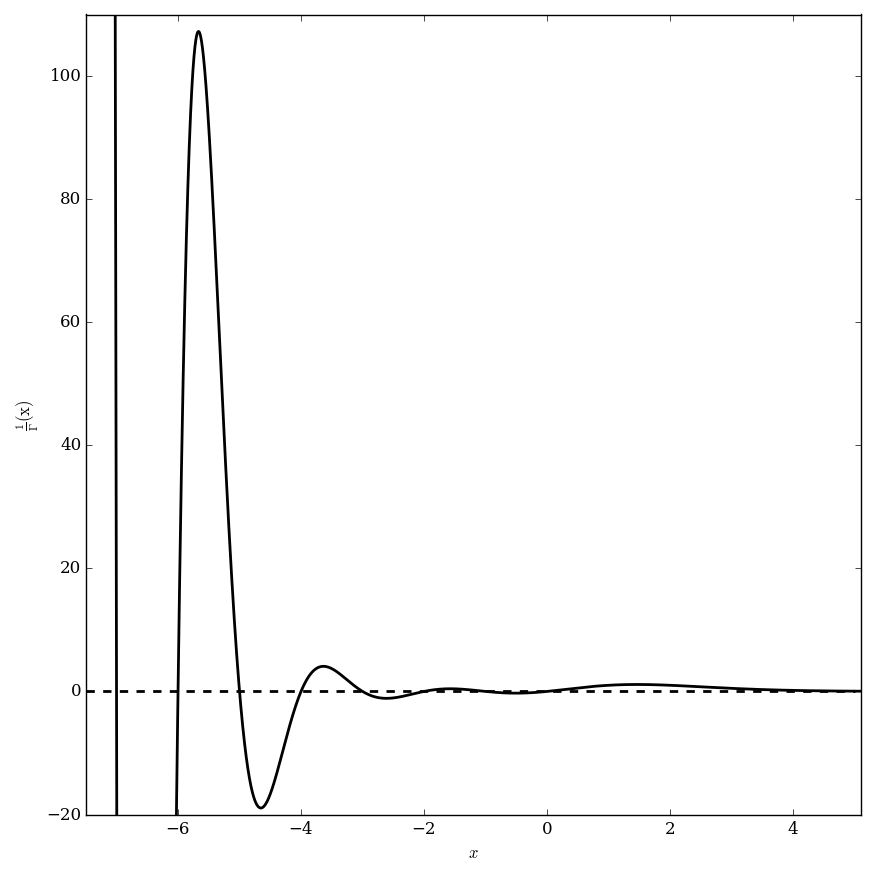
| + | File:Reciprocalgammaplotonneg7.5to5.1.png|Graph of $\dfrac{1}{\Gamma}$ on $[-7.5,5.1]$. | ||
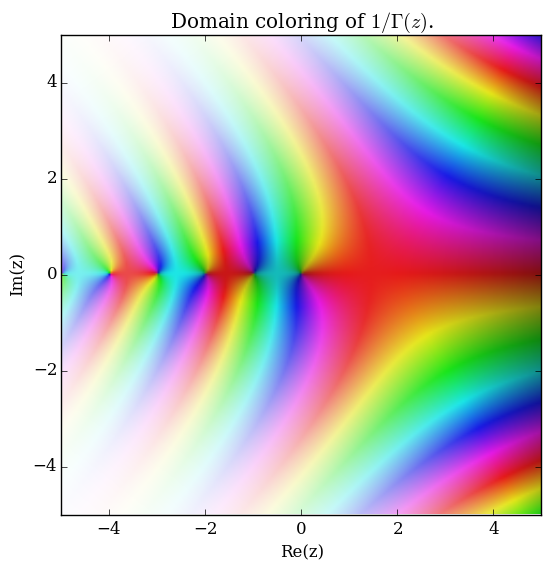
| + | File:Complexreciprocalgammaplot.png|[[Domain coloring]] of $\dfrac{1}{\Gamma}$. | ||
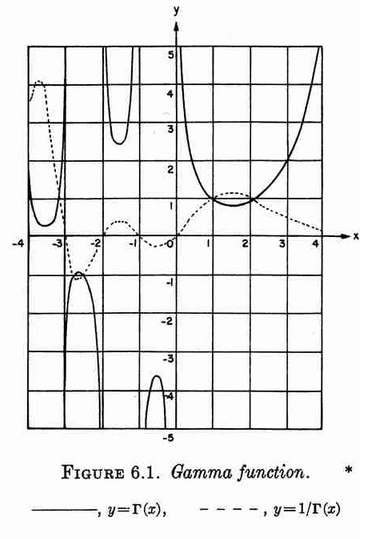
| + | File:Gamma and reciprocal gamma (abramowitzandstegun).png|Plot of [[Gamma function|$\Gamma$]] and $\dfrac{1}{\Gamma}$ from Abramowitz&Stegun. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
| + | =Properties= | ||
| + | [[Reciprocal gamma is entire]]<br /> | ||
| + | [[Reciprocal gamma written as an infinite product]]<br /> | ||
| + | [[Contour integral representation of reciprocal gamma]]<br /> | ||
| + | |||
| + | =See Also= | ||
| + | [[Fransén–Robinson constant]]<br /> | ||
| + | [[Gamma function]] <br /> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 10:50, 11 January 2017
The reciprocal gamma function $\dfrac{1}{\Gamma}$ is defined by $$\left( \dfrac{1}{\Gamma} \right)(z) =\dfrac{1}{\Gamma(z)},$$ where $\Gamma$ denotes the gamma function.
Graph of $\dfrac{1}{\Gamma}$ on $[-4,10]$.
Graph of $\dfrac{1}{\Gamma}$ on $[-7.5,5.1]$.
Domain coloring of $\dfrac{1}{\Gamma}$.
Plot of $\Gamma$ and $\dfrac{1}{\Gamma}$ from Abramowitz&Stegun.
.png)
Properties
Reciprocal gamma is entire
Reciprocal gamma written as an infinite product
Contour integral representation of reciprocal gamma
