Difference between revisions of "Binomial coefficient"

From specialfunctionswiki
Jump to: navigation, search
 
(18 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
The binomial coefficients are defined by the formula
+
The binomial coefficient ${n \choose k}$ are defined for non-negative $n$ and $k$ by the formula
−
$${}_nC_k:={n \choose k} = \dfrac{n!}{(n-k)!k!}.$$
+
$${n \choose k} = \dfrac{n!}{(n-k)!k!},$$
 +
where $n!$ denotes the [[factorial]]. More generally, if $\alpha \in \mathbb{C}$ we define the (generalized) binomial coefficient by
 +
$${\alpha \choose k} = \dfrac{\alpha^{\underline{k}}}{k!},$$
 +
where $\alpha^{\underline{k}}$ denotes the [[falling factorial]].
 +
 
 +
<div align="center">
 +
<gallery>
 +
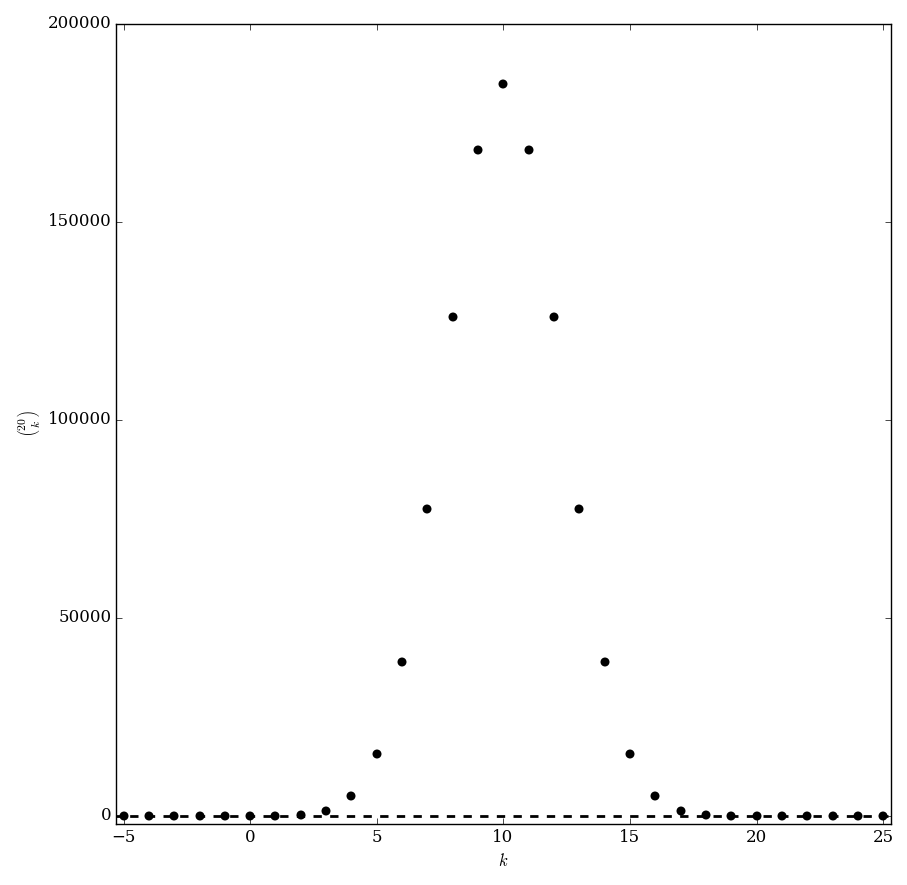
File:Binomialcoefficient,n=20plot.png|Graph of $\displaystyle{20 \choose k}$.
 +
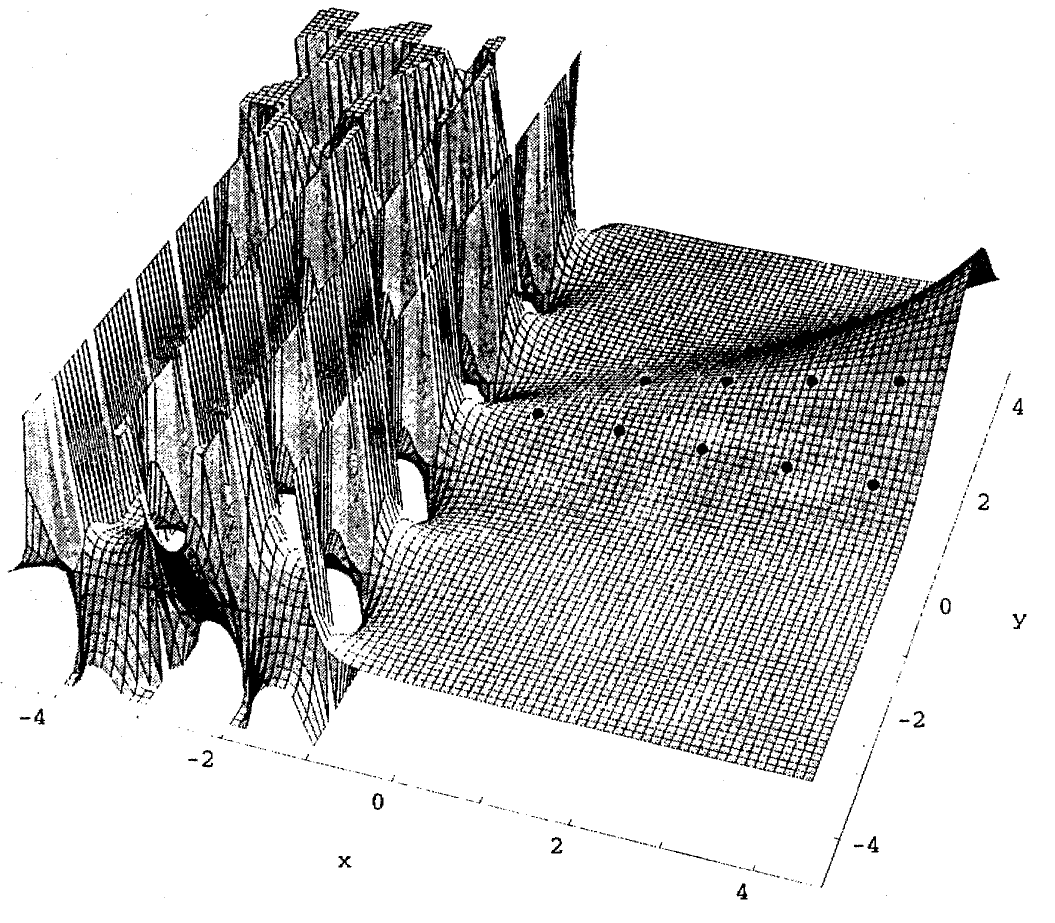
File:Binomialcoefficientfunction.png|Graph of the complex binomial coefficient function.
 +
</gallery>
 +
</div>
  
 
=Properties=
 
=Properties=
−
<div class="toccolours mw-collapsible mw-collapsed">
+
[[Binomial theorem]]<br />
−
<strong>Theorem (Binomial Theorem):</strong> $(a+b)^n = \displaystyle\sum_{k=0}^n {n \choose k} a^k b^{n-k}$
+
[[Binomial series]]<br />
−
<div class="mw-collapsible-content">
+
[[Binomial coefficient (n choose k) equals (n choose (n-k))]]<br />
−
<strong>Proof:</strong> █
+
[[Binomial coefficient (n choose k) equals (-1)^k ((k-n-1) choose k)]]<br />
−
</div>
+
[[Binomial coefficient ((n+1) choose k) equals (n choose k) + (n choose (k-1))]]<br />
−
</div>
+
[[Binomial coefficient (n choose 0) equals 1]]<br />
 +
[[Binomial coefficient (n choose n) equals 1]]<br />
 +
[[Sum over bottom of binomial coefficient with top fixed equals 2^n]]<br />
 +
[[Alternating sum over bottom of binomial coefficient with top fixed equals 0]]<br />
 +
 
 +
=Videos=
 +
[https://www.youtube.com/watch?v=OMr9ZF1jgNc Pascal's Triangle and the Binomial Coefficients]<br />
 +
[https://www.youtube.com/watch?v=MVmgsATTg2I Example of choose function (Binomial Coefficient)]<br />
 +
[https://www.youtube.com/watch?v=lGow-vogneQ Binomial coefficients]<br />
  
 
=References=
 
=References=
−
[http://dualaud.net/specialfunctionswiki/abramowitz_and_stegun-1.03/page_10.htm Abramowitz and Stegun]
+
* {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Binomial theorem|next=Binomial coefficient (n choose k) equals (n choose (n-k))}}: $3.1.2$
 +
*[http://www.jstor.org/discover/10.2307/2975209?sid=21105065140641&uid=4&uid=70&uid=2&uid=3739256&uid=3739744&uid=2129 The Binomial Coefficient Function]<br />
 +
 
 +
[[Category:SpecialFunction]]

Latest revision as of 18:37, 25 September 2016

The binomial coefficient ${n \choose k}$ are defined for non-negative $n$ and $k$ by the formula $${n \choose k} = \dfrac{n!}{(n-k)!k!},$$ where $n!$ denotes the factorial. More generally, if $\alpha \in \mathbb{C}$ we define the (generalized) binomial coefficient by $${\alpha \choose k} = \dfrac{\alpha^{\underline{k}}}{k!},$$ where $\alpha^{\underline{k}}$ denotes the falling factorial.

  • Graph of $\displaystyle{20 \choose k}$.

  • Graph of the complex binomial coefficient function.

Properties

Binomial theorem
Binomial series
Binomial coefficient (n choose k) equals (n choose (n-k))
Binomial coefficient (n choose k) equals (-1)^k ((k-n-1) choose k)
Binomial coefficient ((n+1) choose k) equals (n choose k) + (n choose (k-1))
Binomial coefficient (n choose 0) equals 1
Binomial coefficient (n choose n) equals 1
Sum over bottom of binomial coefficient with top fixed equals 2^n
Alternating sum over bottom of binomial coefficient with top fixed equals 0

Videos

Pascal's Triangle and the Binomial Coefficients
Example of choose function (Binomial Coefficient)
Binomial coefficients

References

Retrieved from "http://specialfunctionswiki.org/index.php?title=Binomial_coefficient&oldid=7560"