Difference between revisions of "Legendre P"
From specialfunctionswiki
m (Tom moved page Legendre polynomial to Legendre P) |
|||
| (11 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The Legendre polynomials are [[orthogonal polynomials]] defined by the | + | The Legendre polynomials are [[orthogonal polynomials]] defined by the formula |
| − | $$P_n(x) = \dfrac{1}{2^ | + | $$P_n(x) = \dfrac{1}{2^n} \displaystyle\sum_{k=0}^n {n \choose k}^2 (x-1)^{n-k}(x+1)^k.$$ |
| + | |||
$$\begin{array}{ll} | $$\begin{array}{ll} | ||
P_0(x) &= 1 \\ | P_0(x) &= 1 \\ | ||
| Line 6: | Line 7: | ||
P_2(x) &= \dfrac{1}{2}(3x^2-1) \\ | P_2(x) &= \dfrac{1}{2}(3x^2-1) \\ | ||
P_3(x) &= \dfrac{1}{2}(5x^3-3x) \\ | P_3(x) &= \dfrac{1}{2}(5x^3-3x) \\ | ||
| + | P_4(x) &= \dfrac{1}{8}(35x^4-30x^2+3) \\ | ||
| + | P_5(x) &= \dfrac{1}{8}(63x^5-70x^3+15x) \\ | ||
\vdots | \vdots | ||
\end{array}$$ | \end{array}$$ | ||
| − | + | <div align="center"> | |
| + | <gallery> | ||
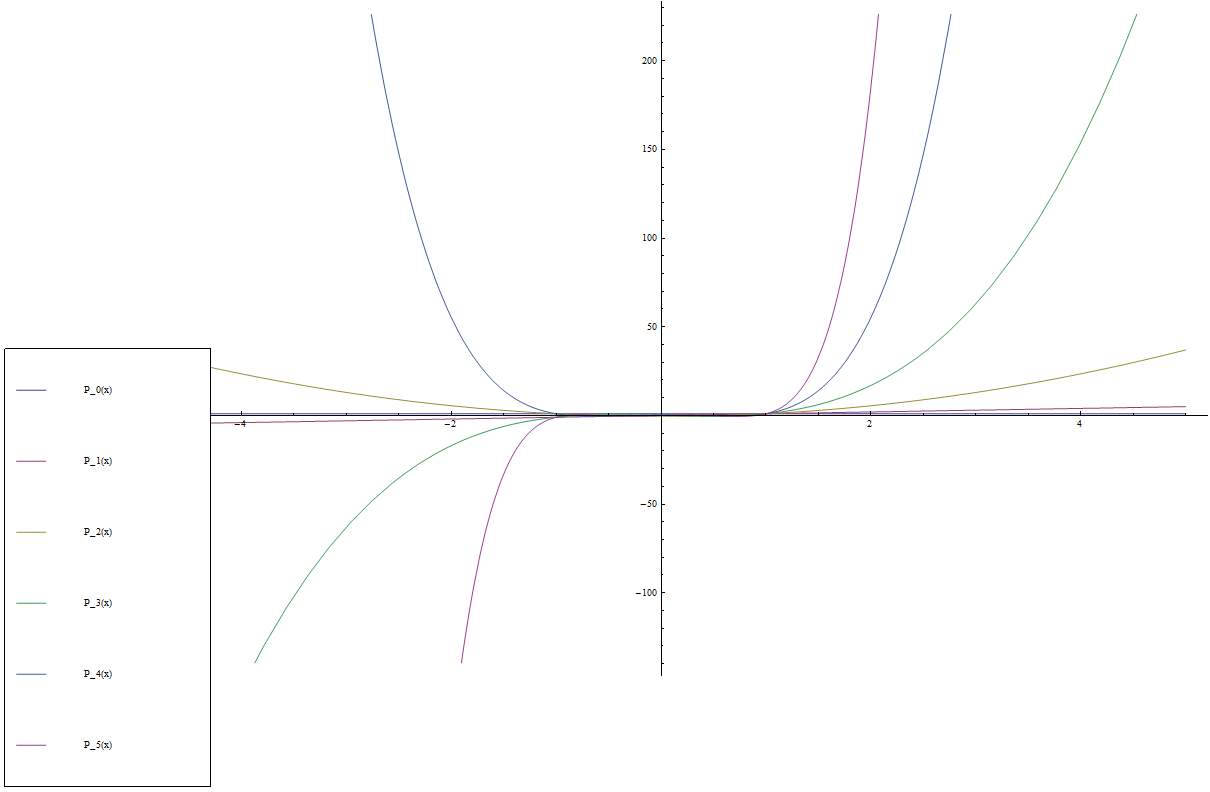
| + | File:Legendrepolynomials.png|Graph of $P_n$ on $[-4,4]$ for $n=0,1,2,3,4,5$. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
| + | =Properties= | ||
| + | [[Relationship between Legendre polynomial and hypergeometric 2F1]]<br /> | ||
| + | |||
| + | {{:Orthogonal polynomials footer}} | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 01:43, 22 June 2016
The Legendre polynomials are orthogonal polynomials defined by the formula $$P_n(x) = \dfrac{1}{2^n} \displaystyle\sum_{k=0}^n {n \choose k}^2 (x-1)^{n-k}(x+1)^k.$$
$$\begin{array}{ll} P_0(x) &= 1 \\ P_1(x) &= x \\ P_2(x) &= \dfrac{1}{2}(3x^2-1) \\ P_3(x) &= \dfrac{1}{2}(5x^3-3x) \\ P_4(x) &= \dfrac{1}{8}(35x^4-30x^2+3) \\ P_5(x) &= \dfrac{1}{8}(63x^5-70x^3+15x) \\ \vdots \end{array}$$
Graph of $P_n$ on $[-4,4]$ for $n=0,1,2,3,4,5$.
Properties
Relationship between Legendre polynomial and hypergeometric 2F1
