Difference between revisions of "Devil's staircase"
From specialfunctionswiki
| (8 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The Devil's staircase | + | The Devil's staircase (also known as the Cantor function) is a function $c \colon [0,1] \rightarrow [0,1]$ can be expressed by the following rules: |
# Write $x$ in base-3. | # Write $x$ in base-3. | ||
# If that representation of $x$ contains a $1$, replace every digit after the first $1$ with $0$'s. | # If that representation of $x$ contains a $1$, replace every digit after the first $1$ with $0$'s. | ||
| Line 10: | Line 10: | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| + | |||
| + | =Properties= | ||
| + | [[Devil's staircase is continuous]]<br /> | ||
| + | [[Devil's staircase is not absolutely continuous]]<br /> | ||
| + | |||
| + | =Videos= | ||
| + | [https://www.youtube.com/watch?v=dQXVn7pFsVI The Devil's Staircase | Infinite Series (19 May 2017)]<br /> | ||
| + | [https://www.youtube.com/watch?v=Hv3fxroMt1s Devil's Staircase (19 February 2017)]<br /> | ||
| + | [https://www.youtube.com/watch?v=TFwiU3W_HoI Intro Real Analysis, Lec 15, Uniform Continuity, Monotone Functions, Devil's Staircase, Derivatives (5 October 2016)]<br /> | ||
| + | [https://www.youtube.com/watch?v=sjfgim3hrno Cantor's staircase (25 November 2014)]<br /> | ||
=References= | =References= | ||
| − | [ | + | |
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 16:03, 10 July 2017
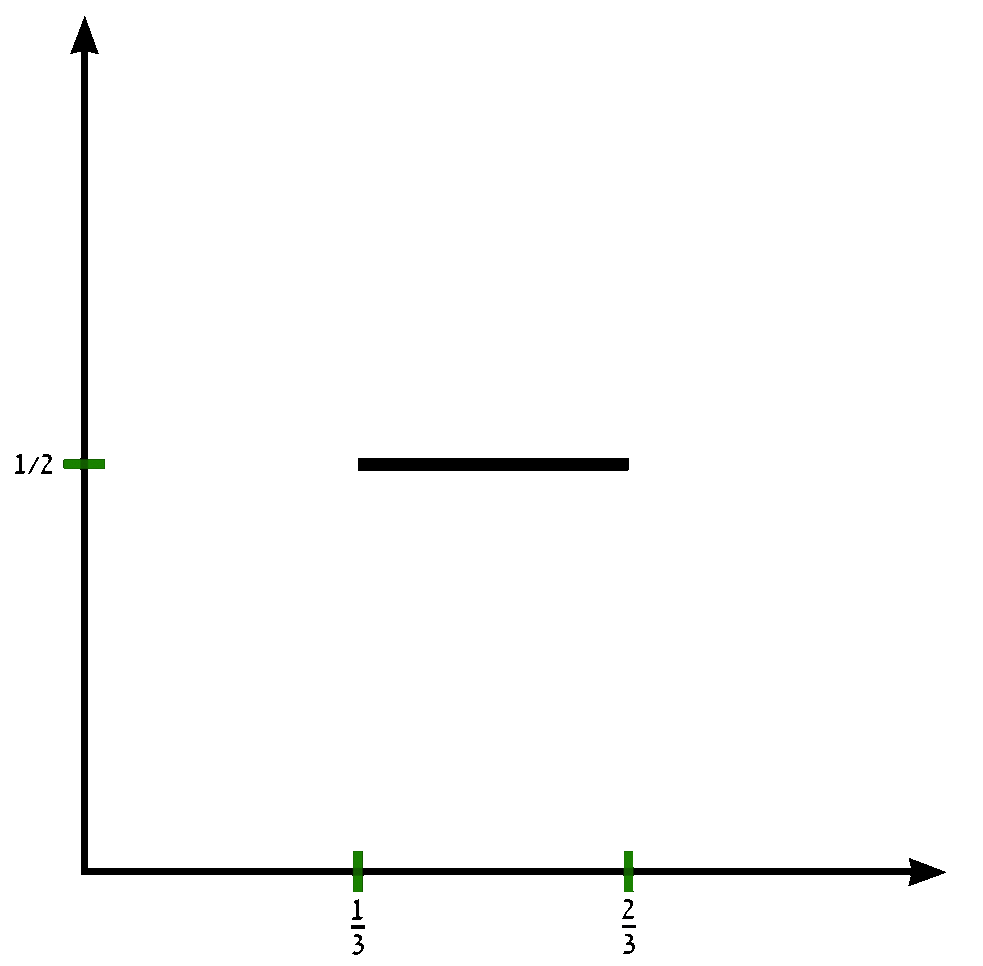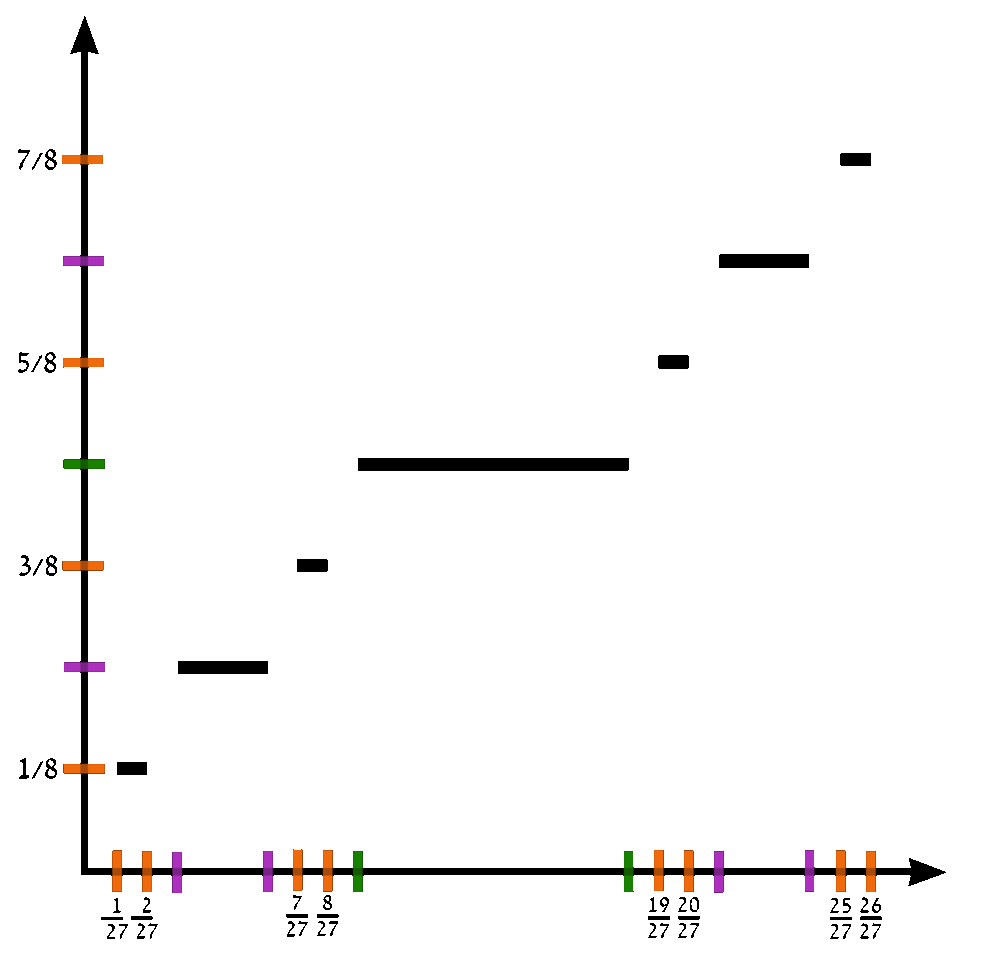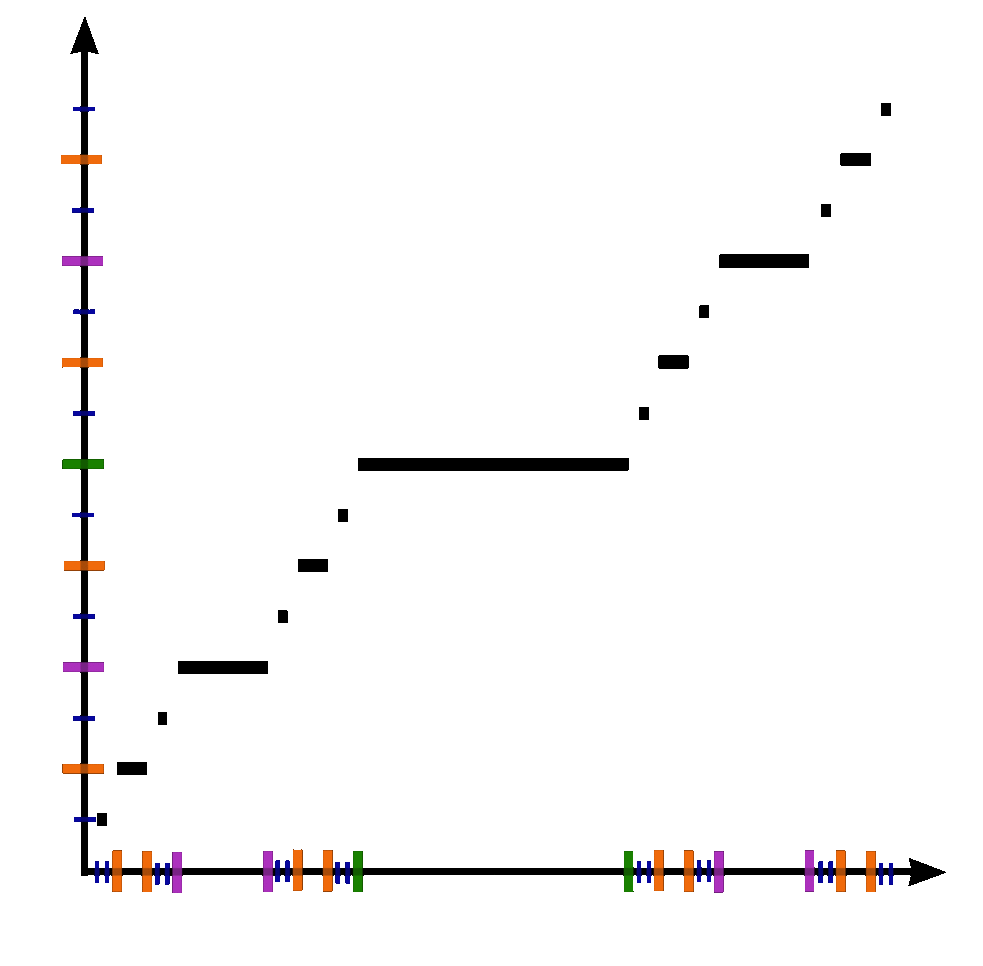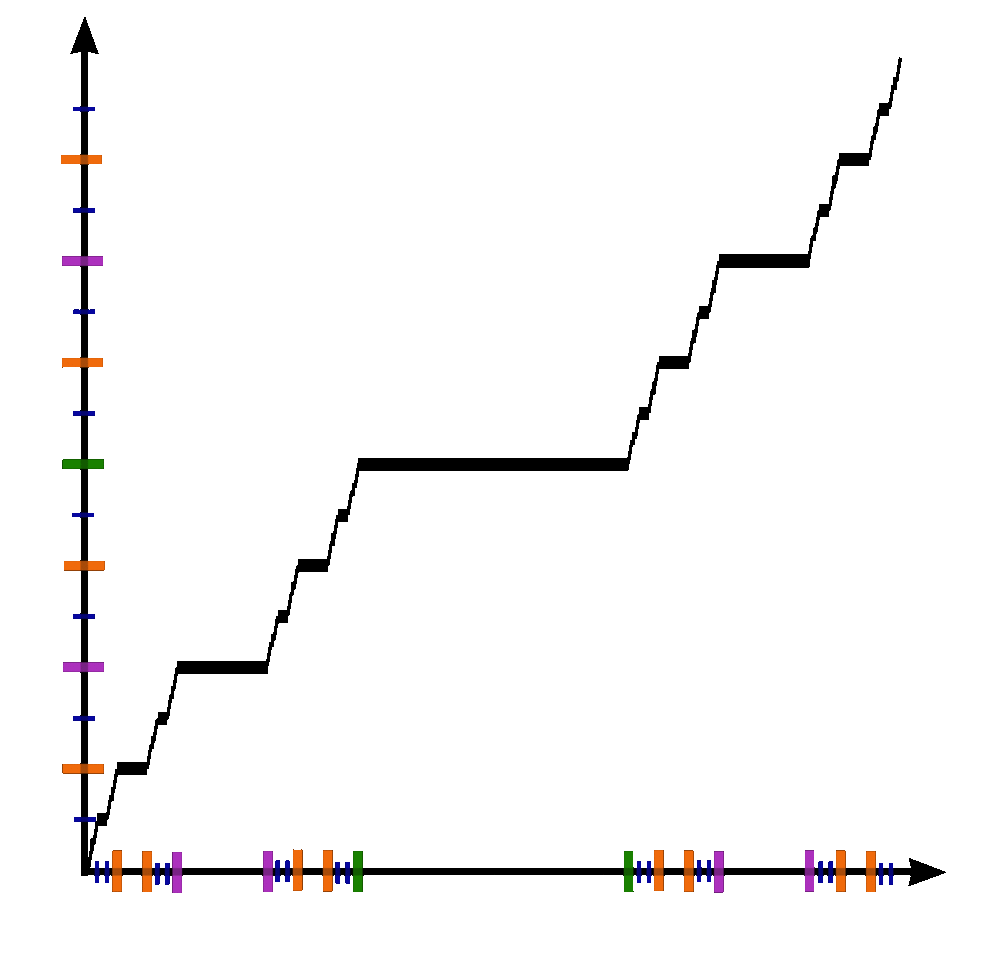
The Devil's staircase (also known as the Cantor function) is a function $c \colon [0,1] \rightarrow [0,1]$ can be expressed by the following rules:
- Write $x$ in base-3.
- If that representation of $x$ contains a $1$, replace every digit after the first $1$ with $0$'s.
- Replace all $2$'s with $1$'s.
- The resulting expansion defines $c(x)$.
Properties
Devil's staircase is continuous
Devil's staircase is not absolutely continuous
Videos
The Devil's Staircase | Infinite Series (19 May 2017)
Devil's Staircase (19 February 2017)
Intro Real Analysis, Lec 15, Uniform Continuity, Monotone Functions, Devil's Staircase, Derivatives (5 October 2016)
Cantor's staircase (25 November 2014)