Difference between revisions of "Jacobi dn"
From specialfunctionswiki
| (8 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Let $u=\displaystyle\int_0^x \dfrac{1}{\sqrt{(1-t^2)(1-mt^2)}}dt = \displaystyle\int_0^{\phi} \dfrac{1}{\sqrt{1-m\sin^2 \theta}} d\theta.$ Then we define | Let $u=\displaystyle\int_0^x \dfrac{1}{\sqrt{(1-t^2)(1-mt^2)}}dt = \displaystyle\int_0^{\phi} \dfrac{1}{\sqrt{1-m\sin^2 \theta}} d\theta.$ Then we define | ||
$$\mathrm{dn \hspace{2pt}} u = \sqrt{1-m\sin^2 \phi} = \sqrt{1-mx^2}.$$ | $$\mathrm{dn \hspace{2pt}} u = \sqrt{1-m\sin^2 \phi} = \sqrt{1-mx^2}.$$ | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
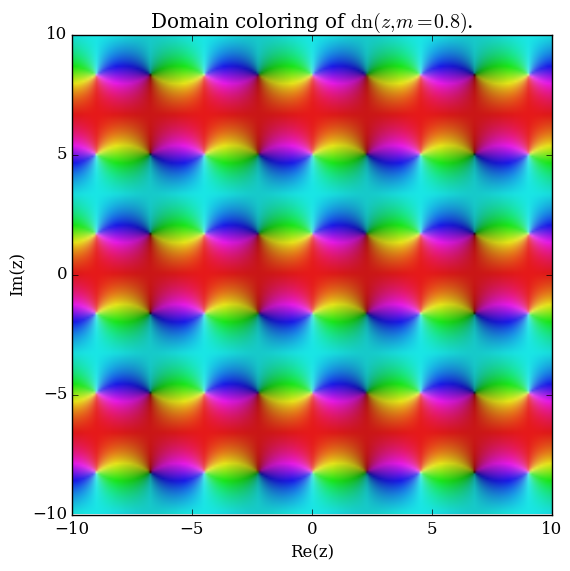
| + | File:Complexjacobidn,m=0.8plot.png|[[Domain coloring]] of $\mathrm{dn}$ corresponding to $m=0.8$. | ||
| + | </gallery> | ||
| + | </div> | ||
=Properties= | =Properties= | ||
#$m \mathrm{sn \hspace{2pt}}^2 u + \mathrm{dn \hspace{2pt}}^2u=1$ | #$m \mathrm{sn \hspace{2pt}}^2 u + \mathrm{dn \hspace{2pt}}^2u=1$ | ||
| + | #$\mathrm{dn \hspace{2pt}}(0)=1$ | ||
| + | #$\dfrac{d \phi}{du} = \mathrm{dn \hspace{2pt}}u$ | ||
| + | #$\dfrac{d}{du}\mathrm{sn \hspace{2pt}} u =\mathrm{cn \hspace{2pt}}(u)\mathrm{dn \hspace{2pt}}(u)$ | ||
| + | |||
| + | =References= | ||
| + | [http://web.mst.edu/~lmhall/SPFNS/spfns.pdf Special functions by Leon Hall] | ||
| + | |||
| + | {{:Jacobi elliptic functions footer}} | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 19:06, 5 July 2016
Let $u=\displaystyle\int_0^x \dfrac{1}{\sqrt{(1-t^2)(1-mt^2)}}dt = \displaystyle\int_0^{\phi} \dfrac{1}{\sqrt{1-m\sin^2 \theta}} d\theta.$ Then we define $$\mathrm{dn \hspace{2pt}} u = \sqrt{1-m\sin^2 \phi} = \sqrt{1-mx^2}.$$
Domain coloring of $\mathrm{dn}$ corresponding to $m=0.8$.
Properties
- $m \mathrm{sn \hspace{2pt}}^2 u + \mathrm{dn \hspace{2pt}}^2u=1$
- $\mathrm{dn \hspace{2pt}}(0)=1$
- $\dfrac{d \phi}{du} = \mathrm{dn \hspace{2pt}}u$
- $\dfrac{d}{du}\mathrm{sn \hspace{2pt}} u =\mathrm{cn \hspace{2pt}}(u)\mathrm{dn \hspace{2pt}}(u)$
References
Special functions by Leon Hall