Difference between revisions of "Arcsec"
From specialfunctionswiki
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | [[File: | + | The [[function]] $\mathrm{arcsec} \colon \mathbb{R} \setminus (-1,1) \rightarrow [0,\pi] \setminus \left\{ \dfrac{\pi}{2} \right\}$ is the [[inverse function]] of the [[secant]] function. |
| + | <div align="center"> | ||
| + | <gallery> | ||
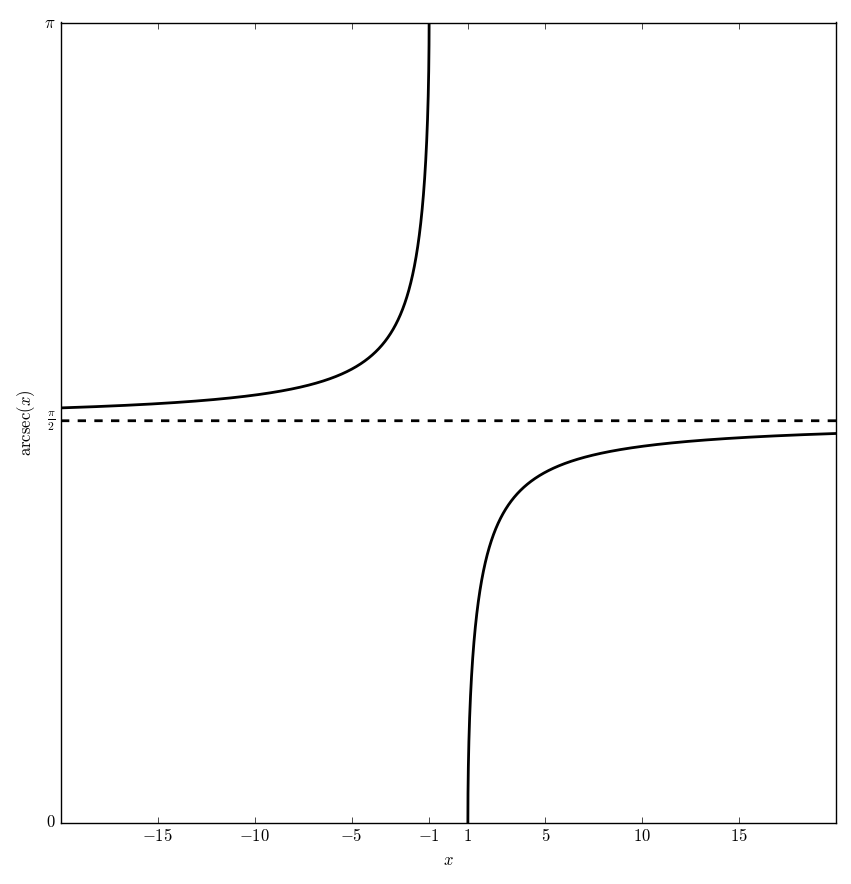
| + | File:Arcsecplot.png|Graph of $\mathrm{arcsec}$. | ||
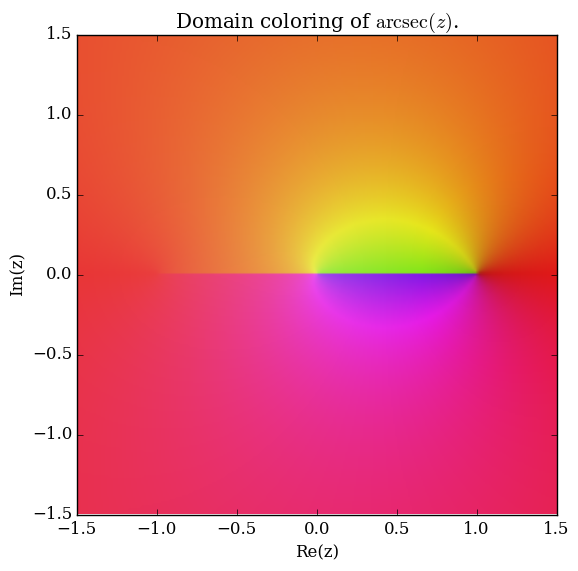
| + | File:Complexarcsecplot.png|[[Domain coloring]] of $\mathrm{arcsec}$. | ||
| + | </gallery> | ||
| + | </div> | ||
=Properties= | =Properties= | ||
| − | + | [[Derivative of arcsec]] | |
| − | < | + | |
| − | + | =See Also= | |
| − | + | [[Secant]] <br /> | |
| − | + | [[Sech]] <br /> | |
| − | + | [[Arcsech]] | |
| − | + | ||
| + | {{:Inverse trigonometric functions footer}} | ||
| − | + | [[Category:SpecialFunction]] | |
Latest revision as of 03:44, 6 July 2016
The function $\mathrm{arcsec} \colon \mathbb{R} \setminus (-1,1) \rightarrow [0,\pi] \setminus \left\{ \dfrac{\pi}{2} \right\}$ is the inverse function of the secant function.
Graph of $\mathrm{arcsec}$.
Domain coloring of $\mathrm{arcsec}$.
