Difference between revisions of "Thomae function"
From specialfunctionswiki
| (12 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Thomae's function is given by the formula | + | __NOTOC__ |
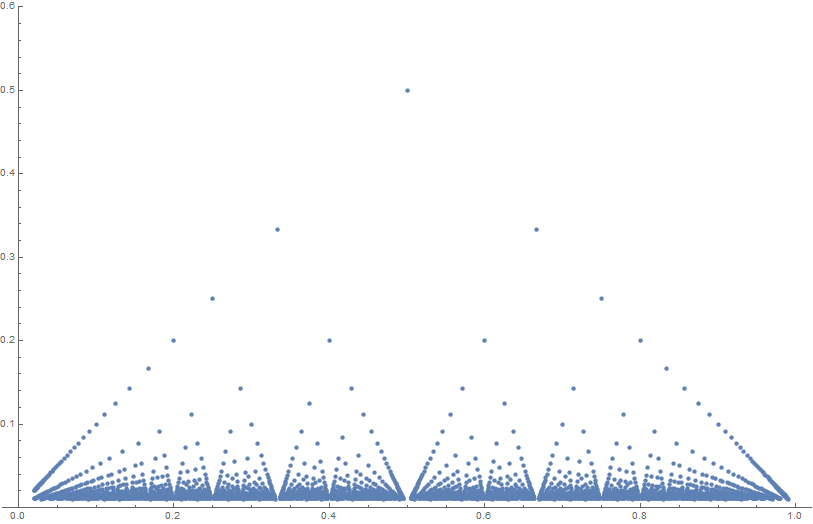
| + | Thomae's function (sometimes called the popcorn function, raindrop function, Stars over Babylon) is given by the formula | ||
$$f(x) =\begin{cases} | $$f(x) =\begin{cases} | ||
1 & \text{if } x= 0 \\ | 1 & \text{if } x= 0 \\ | ||
| Line 12: | Line 13: | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| + | |||
| + | =Properties= | ||
| + | [[Thomae function is continuous at irrationals]]<br /> | ||
| + | [[Thomae function is discontinuous at rationals]]<br /> | ||
| + | |||
| + | =Videos= | ||
| + | [https://www.youtube.com/watch?v=Xu5Y6DqzN7Q Thomae Function by Bret Benesh (11 January 2012)]<br /> | ||
| + | [https://www.youtube.com/watch?v=HeIU5lLtHyQ Thomae Function by Douglas Harder (19 April 2012)]<br /> | ||
| + | |||
| + | =See also= | ||
| + | [https://kbeanland.files.wordpress.com/2010/01/beanlandrobstevensonmonthly.pdf Modifications of Thomae's Function and Differentiability] | ||
| + | |||
| + | =References= | ||
| + | [https://www.math.washington.edu/~morrow/334_10/thomae.pdf]<br /> | ||
| + | [https://math.la.asu.edu/~kuiper/371files/ThomaeFunction.pdf]<br /> | ||
| + | [http://math.stackexchange.com/questions/530097/proof-of-continuity-of-thomae-function-at-irrationals]<br /> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 00:36, 9 December 2016
Thomae's function (sometimes called the popcorn function, raindrop function, Stars over Babylon) is given by the formula $$f(x) =\begin{cases} 1 & \text{if } x= 0 \\ \tfrac1{q} & \text{if } x = \tfrac{p}{q}\\ 0 & \text{if } x \in \mathbb{R}-\mathbb{Q}. \end{cases}$$
Properties
Thomae function is continuous at irrationals
Thomae function is discontinuous at rationals
Videos
Thomae Function by Bret Benesh (11 January 2012)
Thomae Function by Douglas Harder (19 April 2012)
See also
Modifications of Thomae's Function and Differentiability