Difference between revisions of "Modified Bessel I"
From specialfunctionswiki
(Created page with "The modified Bessel function of the first kind is defined by $$I_{\nu}(z)=i^{-\nu}J_{\nu}(iz).$$") |
|||
| (27 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
The modified Bessel function of the first kind is defined by | The modified Bessel function of the first kind is defined by | ||
| − | $$I_{\nu}(z)=i^{-\nu}J_{\nu}(iz).$$ | + | $$I_{\nu}(z)=i^{-\nu}J_{\nu}(iz),$$ |
| + | where $i$ denotes the [[imaginary number]] and $J_{\nu}$ denotes the [[Bessel J|Bessel function of the first kind]]. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
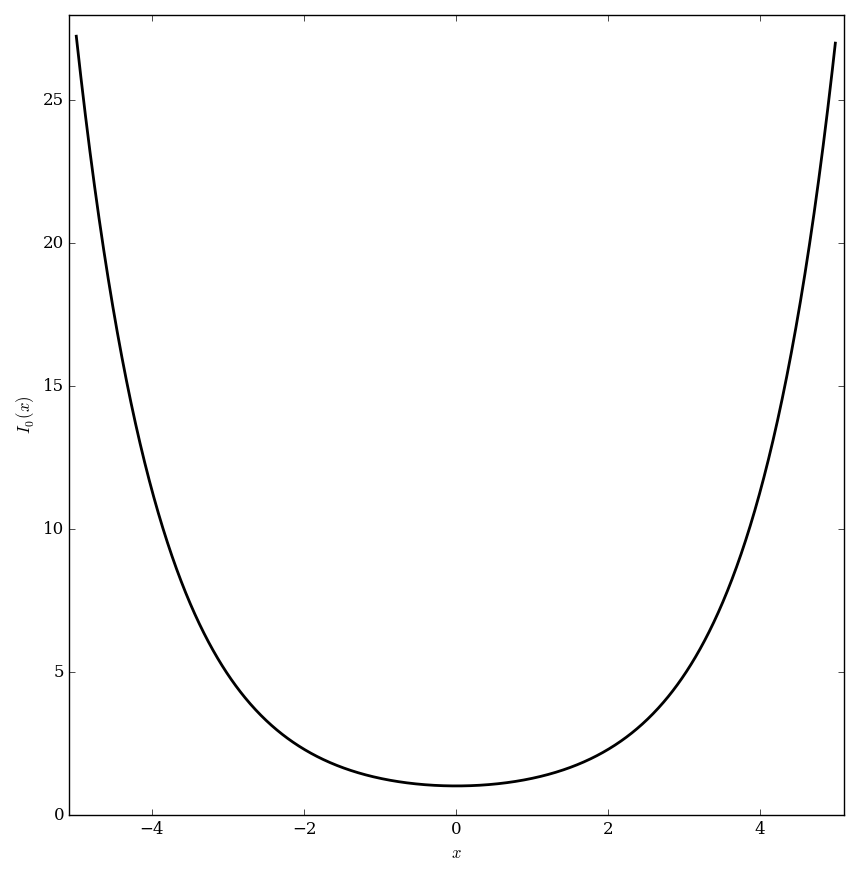
| + | File:Besseli,n=0plot.png|Graph of $I_0$. | ||
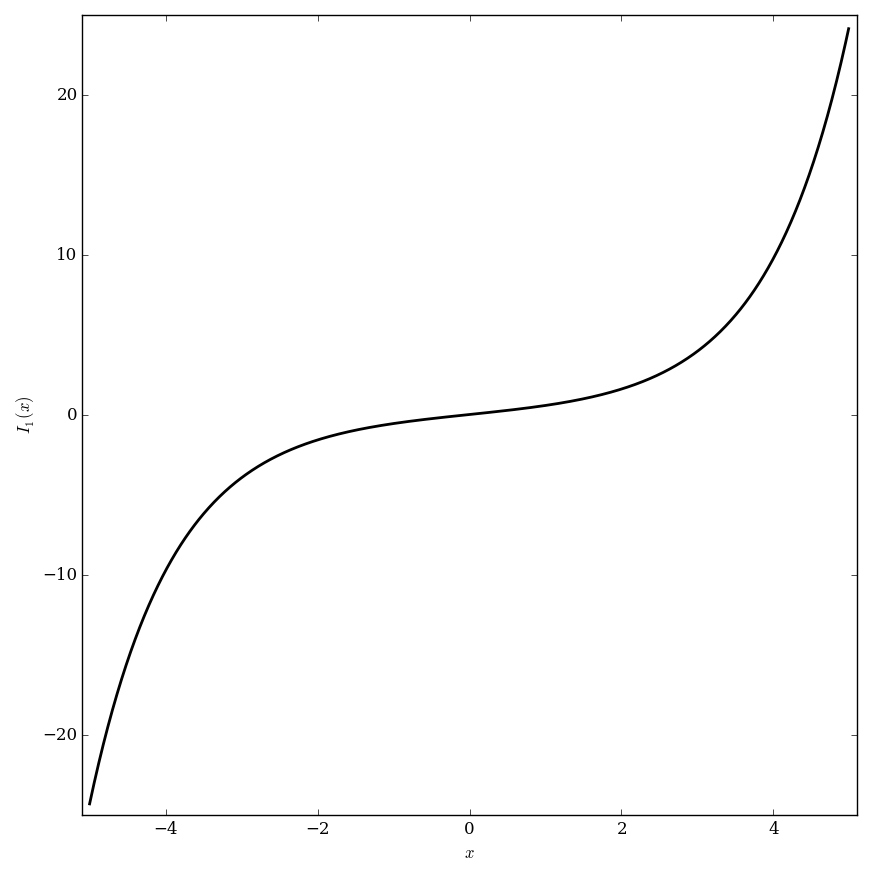
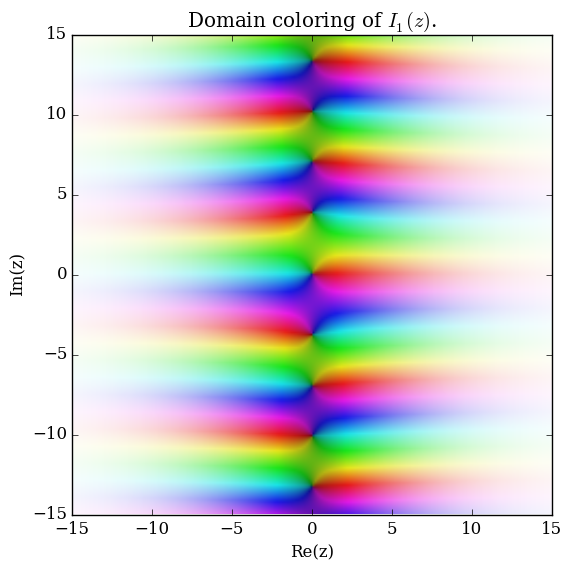
| + | File:Besseli,n=1plot.png|Graph of $I_1$. | ||
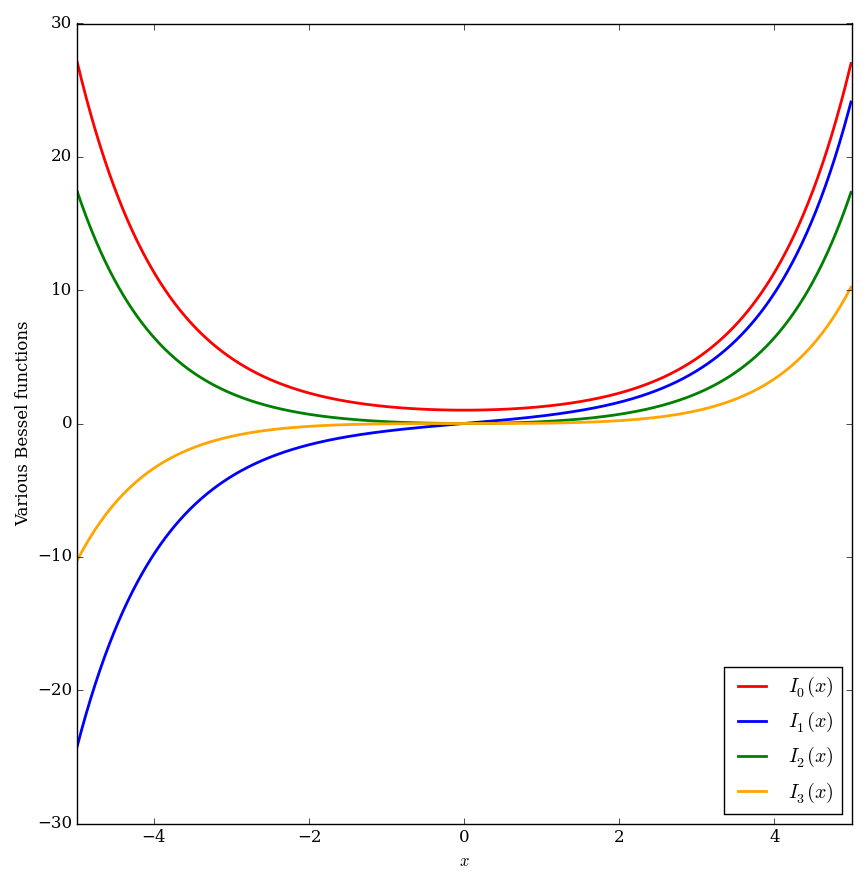
| + | File:Multiplebesseliplot.png|Graph of $I_0$,$I_1$,$I_2$, and $I_3$. | ||
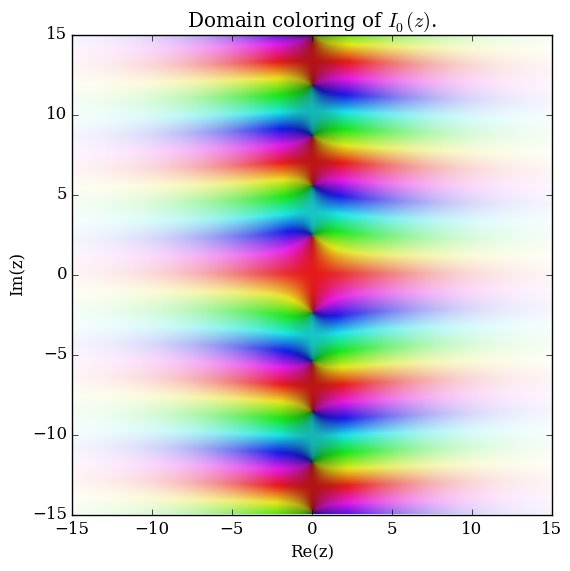
| + | File:Complexbesseli,n=0plot.png|[[Domain coloring]] of $I_0$. | ||
| + | File:Complexbesseli,n=1plot.png|[[Domain coloring]] of $I_0$. | ||
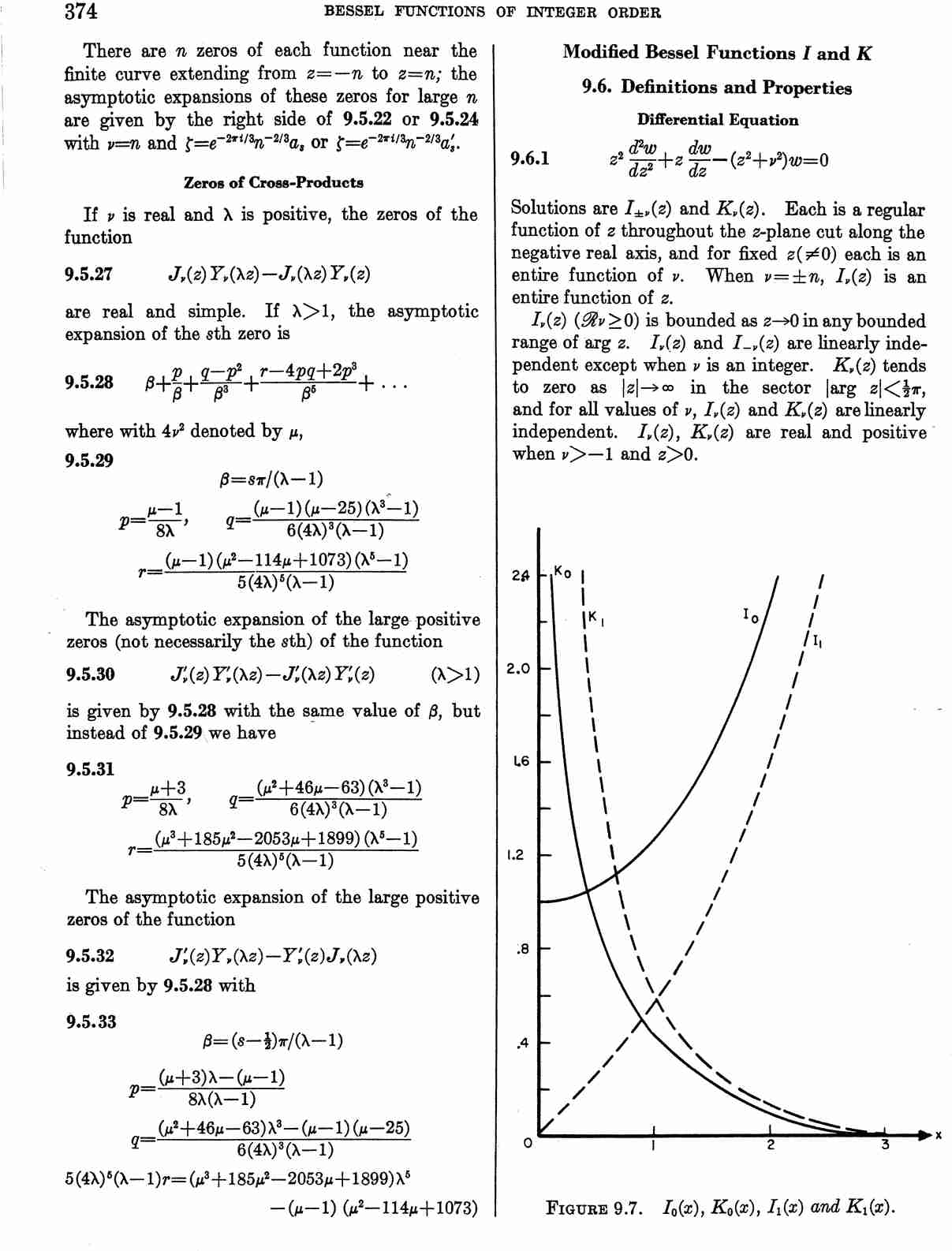
| + | File:Page 374 (Abramowitz&Stegun).jpg|Modified Bessel functions from Abramowitz&Stegun. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
| + | =Properties= | ||
| + | [[Relationship between Bessel I sub -1/2 and cosh]]<br /> | ||
| + | [[Relationship between Bessel I sub 1/2 and sinh]]<br /> | ||
| + | [[Relationship between Bessel I sub n and Bessel J sub n]]<br /> | ||
| + | [[Relationship between Airy Bi and modified Bessel I]]<br /> | ||
| + | |||
| + | =References= | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
| + | |||
| + | {{:Bessel functions footer}} | ||
Latest revision as of 23:53, 10 June 2016
The modified Bessel function of the first kind is defined by $$I_{\nu}(z)=i^{-\nu}J_{\nu}(iz),$$ where $i$ denotes the imaginary number and $J_{\nu}$ denotes the Bessel function of the first kind.
Domain coloring of $I_0$.
Domain coloring of $I_0$.
Properties
Relationship between Bessel I sub -1/2 and cosh
Relationship between Bessel I sub 1/2 and sinh
Relationship between Bessel I sub n and Bessel J sub n
Relationship between Airy Bi and modified Bessel I