Difference between revisions of "Spherical Hankel h (1)"
From specialfunctionswiki
(Created page with "The spherical Hankel function $h_{\nu}^{(1)}$ is defined by $$h_{\nu}^{(1)}(z)=j_{\nu}(z)+iy_{\nu}(z),$$ where $j_{\nu}$ is the Spherical Bessel j sub nu|spherical Bessel fu...") |
|||
| (10 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
$$h_{\nu}^{(1)}(z)=j_{\nu}(z)+iy_{\nu}(z),$$ | $$h_{\nu}^{(1)}(z)=j_{\nu}(z)+iy_{\nu}(z),$$ | ||
where $j_{\nu}$ is the [[Spherical Bessel j sub nu|spherical Bessel function of the first kind]] and $y_{\nu}$ is the [[Spherical Bessel y sub nu|spherical Bessel function of the second kind]]. | where $j_{\nu}$ is the [[Spherical Bessel j sub nu|spherical Bessel function of the first kind]] and $y_{\nu}$ is the [[Spherical Bessel y sub nu|spherical Bessel function of the second kind]]. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
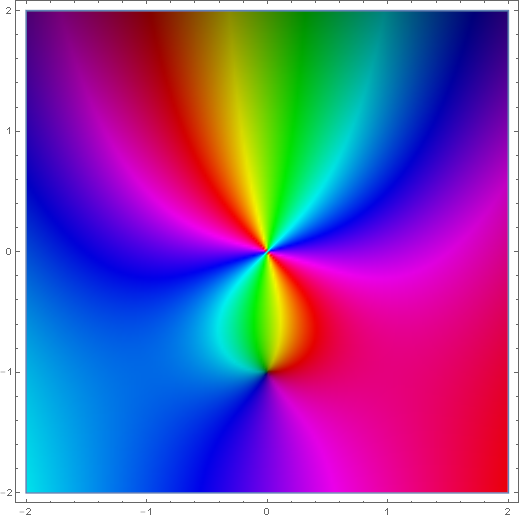
| + | File:Complex spherical hankel h1 sub 1.png|[[Domain coloring]] of $h_1^{(1)}(z)$. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
| + | =See Also= | ||
| + | [[Spherical Bessel j|Spherical Bessel $j$]] <br /> | ||
| + | [[Spherical Bessel y|Spherical Bessel $y$]]<br /> | ||
| + | |||
| + | {{:Hankel functions footer}} | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 23:58, 22 December 2016
The spherical Hankel function $h_{\nu}^{(1)}$ is defined by $$h_{\nu}^{(1)}(z)=j_{\nu}(z)+iy_{\nu}(z),$$ where $j_{\nu}$ is the spherical Bessel function of the first kind and $y_{\nu}$ is the spherical Bessel function of the second kind.
Domain coloring of $h_1^{(1)}(z)$.
See Also
Spherical Bessel $j$
Spherical Bessel $y$