Difference between revisions of "Bessel J"
(→Properties) |
|||
| (31 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The Bessel functions of the first kind, $J_{\nu}$ | + | __NOTOC__ |
| − | $$J_{\nu}(z)=\displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k}{k! \Gamma(k+\nu+1)2^{2k+\nu}}z^{2k+\nu} | + | The Bessel functions of the first kind, $J_{\nu} \colon \mathbb{C} \rightarrow \mathbb{C}$ are defined by |
| + | $$J_{\nu}(z)=\displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k}{k! \Gamma(k+\nu+1)2^{2k+\nu}}z^{2k+\nu},$$ | ||
| + | where $\Gamma$ denotes the [[gamma]] function. | ||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
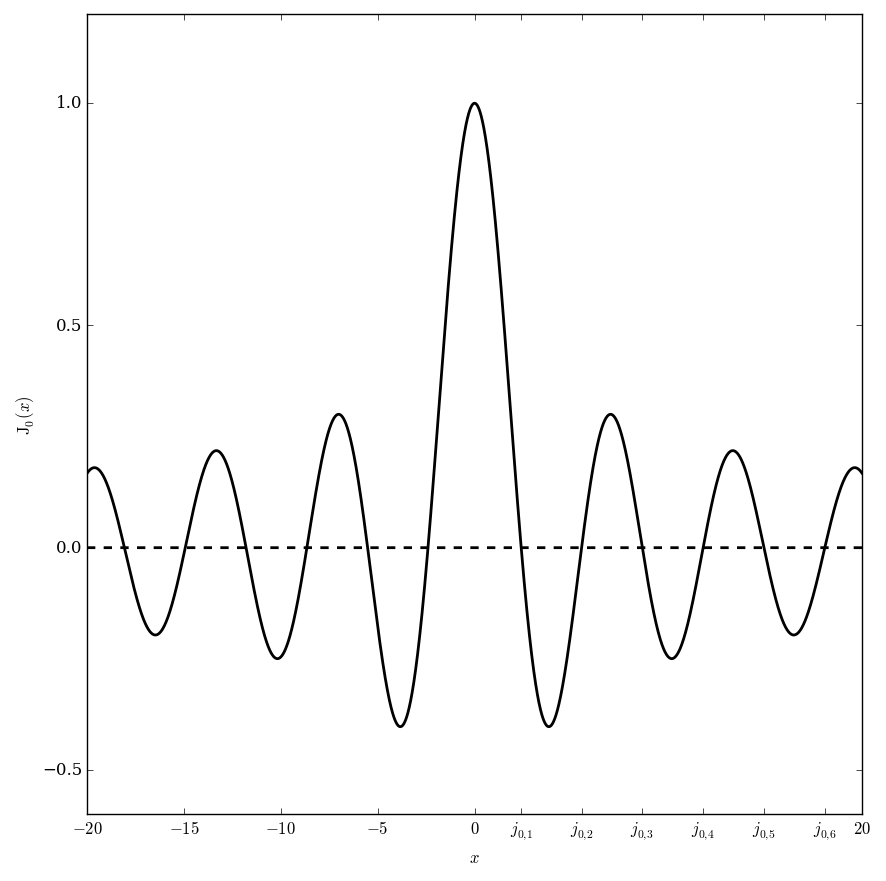
| − | File: | + | File:Besseljn=0plot.png|Graph of $J_0$. |
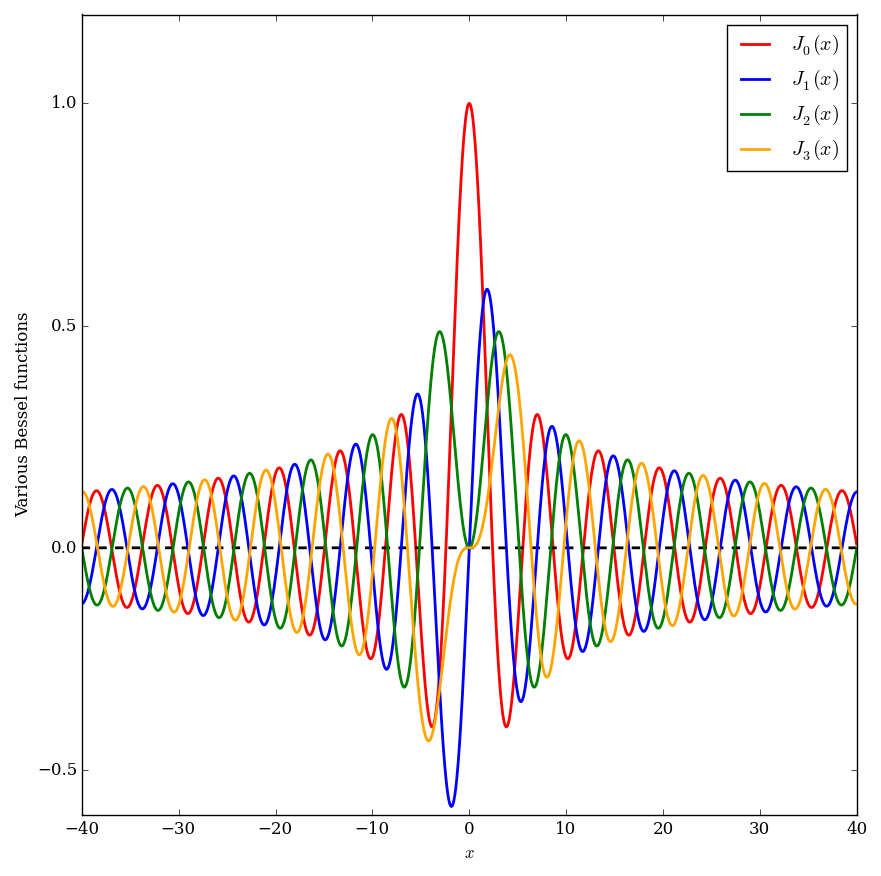
| − | File:Complexbesselj0.png|[[Domain coloring]] of $ | + | File:Multiplebesseljplot.png|Graph of various Bessel functions. |
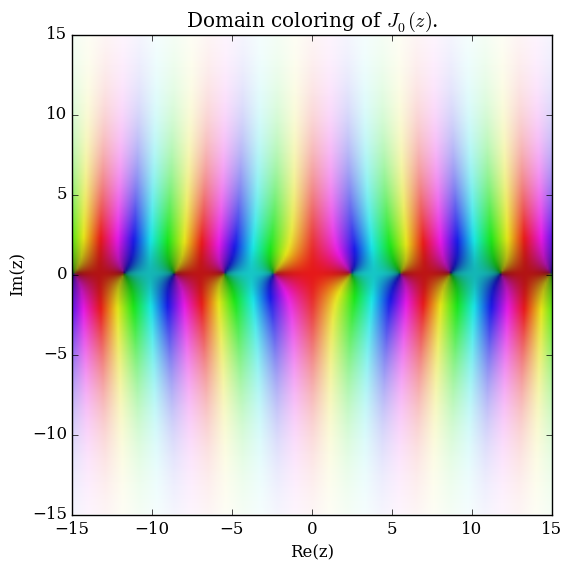
| − | File: | + | File:Complexbesselj0plot.png|[[Domain coloring]] of $J_0$. |
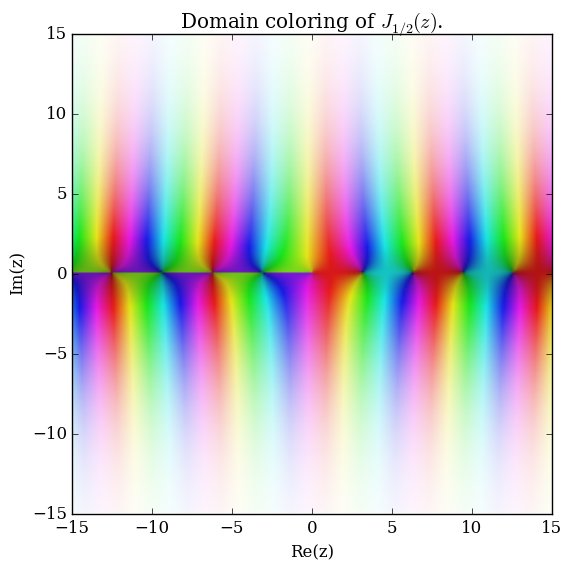
| + | File:Complexbesselj0.5plot.png|[[Domain coloring]] of $J_{\frac{1}{2}}$. | ||
| + | File:Complexbesselj5plot.png|[[Domain coloring]] of $J_5$. | ||
File:Page 359Abramowitz-Stegun(Bessel functions).jpg|Bessel functions from [http://dualaud.net/specialfunctionswiki/abramowitz_and_stegun-1.03/ Abramowitz&Stegun] | File:Page 359Abramowitz-Stegun(Bessel functions).jpg|Bessel functions from [http://dualaud.net/specialfunctionswiki/abramowitz_and_stegun-1.03/ Abramowitz&Stegun] | ||
</gallery> | </gallery> | ||
| Line 12: | Line 16: | ||
=Properties= | =Properties= | ||
| − | + | [[Bessel polynomial in terms of Bessel functions]]<br /> | |
| − | + | [[Bessel at n+1/2 in terms of Bessel polynomial]]<br /> | |
| − | + | [[Bessel at -n-1/2 in terms of Bessel polynomial]]<br /> | |
| − | + | [[Relationship between Bessel J and hypergeometric 0F1]]<br /> | |
| − | + | [[Relationship between Bessel I and Bessel J]]<br /> | |
| − | </ | + | [[Relationship between Anger function and Bessel J]]<br /> |
| − | + | [[Derivative of Bessel J with respect to its order]]<br /> | |
| − | + | [[Integral of monomial times Bessel J]]<br /> | |
| − | + | [[Integral of Bessel J for Re(nu) greater than -1]]<br /> | |
| − | + | [[Integral of Bessel J for nu=2n]]<br /> | |
| − | + | [[Integral of Bessel J for nu=2n+1]]<br /> | |
| − | + | [[Integral of Bessel J for nu=n+1]]<br /> | |
| − | + | [[Integral of Bessel J for nu=1]]<br /> | |
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=Videos= | =Videos= | ||
| Line 79: | Line 40: | ||
[https://www.youtube.com/watch?v=p-_MnYBLkcA Orthogonal Properties of Bessel Function, Orthogonal Properties of Bessel Equation] | [https://www.youtube.com/watch?v=p-_MnYBLkcA Orthogonal Properties of Bessel Function, Orthogonal Properties of Bessel Equation] | ||
| − | =Links= | + | =External Links= |
| − | [http://www.johndcook.com/blog/2013/08/03/addition-formulas-for-bessel-functions/ Addition formulas for Bessel functions]<br /> | + | [http://www.johndcook.com/blog/2013/08/03/addition-formulas-for-bessel-functions/ Addition formulas for Bessel functions by John D. Cook]<br /> |
| − | [http://www.johndcook.com/Bessel_functions.html Relations between Bessel functions by John D. Cook] | + | [http://www.johndcook.com/Bessel_functions.html Relations between Bessel functions by John D. Cook]<br /> |
| + | [http://gdz.sub.uni-goettingen.de/dms/load/img/?PID=PPN600494829_0021%7CLOG_0023 Bessel's functions of the second order - C.V. Coates]<br /> | ||
| + | |||
| + | =References= | ||
| + | * {{BookReference|A Treatise on Bessel Functions|1895|Andrew Gray|author2=G.B. Mathews|prev=findme|next=findme}}: Ch. 2 $10$ | ||
| + | * {{BookReference|Higher Transcendental Functions Volume II|1953|Arthur Erdélyi|author2=Wilhelm Magnus|author3=Fritz Oberhettinger|author4=Francesco G. Tricomi|prev=findme|next=findme}}: $\S 7.2.1 (2)$ | ||
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=findme}}: $9.1.10$ | ||
| + | |||
| + | |||
| + | {{:Bessel functions footer}} | ||
| − | + | [[Category:SpecialFunction]] | |
Latest revision as of 05:41, 4 March 2018
The Bessel functions of the first kind, $J_{\nu} \colon \mathbb{C} \rightarrow \mathbb{C}$ are defined by $$J_{\nu}(z)=\displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k}{k! \Gamma(k+\nu+1)2^{2k+\nu}}z^{2k+\nu},$$ where $\Gamma$ denotes the gamma function.
Domain coloring of $J_0$.
Domain coloring of $J_{\frac{1}{2}}$.
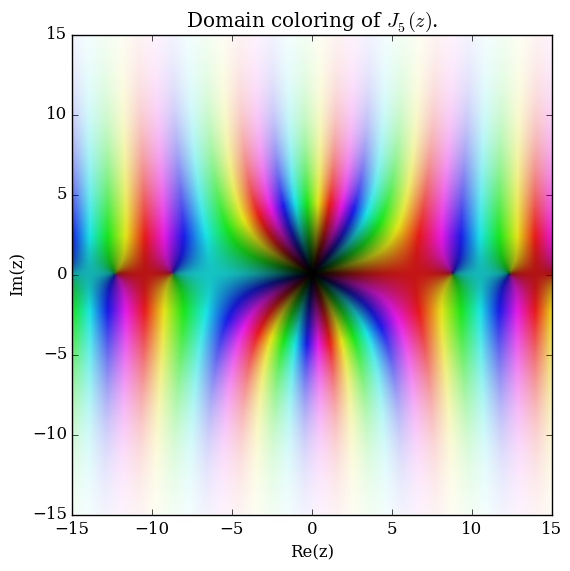
Domain coloring of $J_5$.
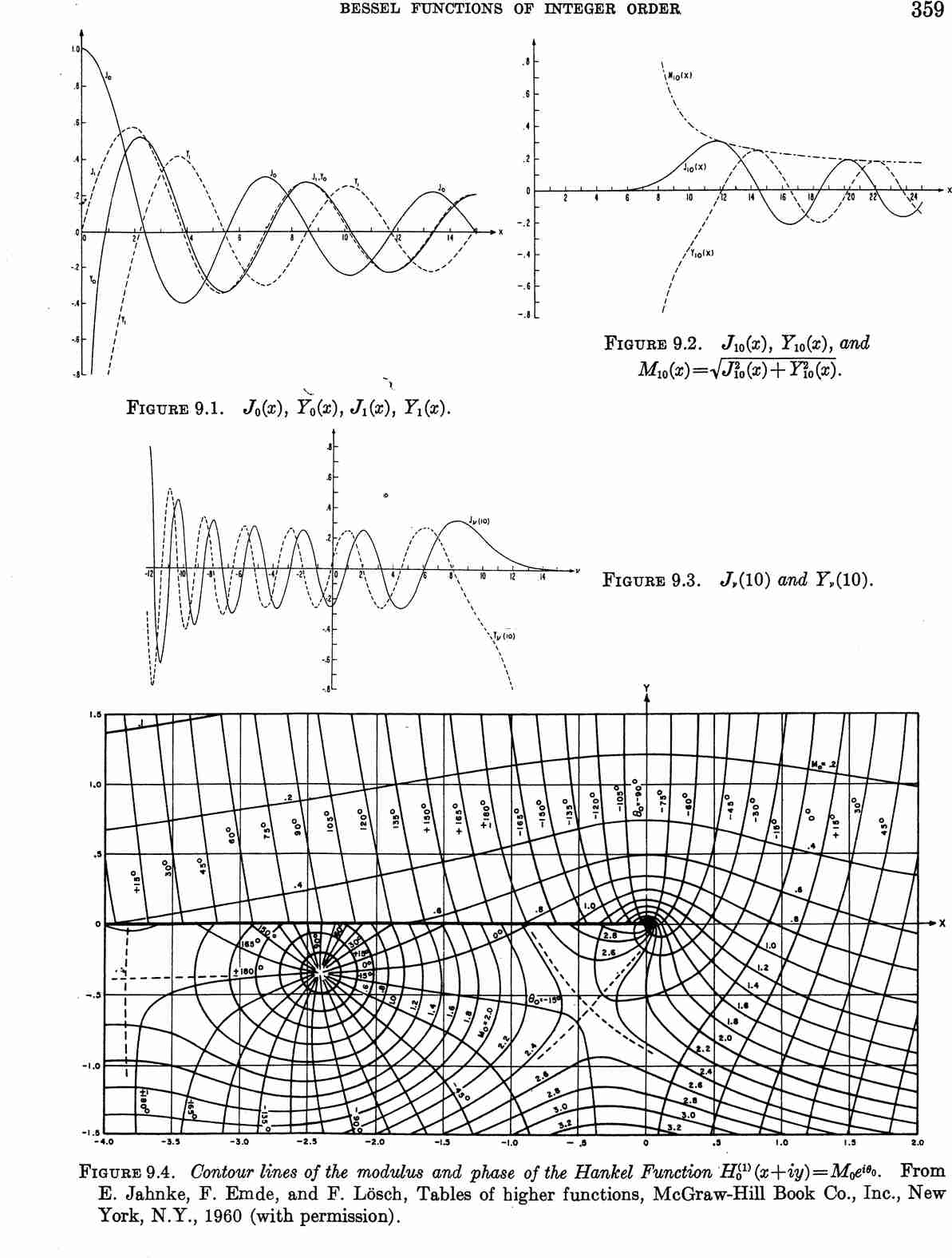
Bessel functions from Abramowitz&Stegun
Properties
Bessel polynomial in terms of Bessel functions
Bessel at n+1/2 in terms of Bessel polynomial
Bessel at -n-1/2 in terms of Bessel polynomial
Relationship between Bessel J and hypergeometric 0F1
Relationship between Bessel I and Bessel J
Relationship between Anger function and Bessel J
Derivative of Bessel J with respect to its order
Integral of monomial times Bessel J
Integral of Bessel J for Re(nu) greater than -1
Integral of Bessel J for nu=2n
Integral of Bessel J for nu=2n+1
Integral of Bessel J for nu=n+1
Integral of Bessel J for nu=1
Videos
Bessel Equation and Bessel functions
Mod-1 Lec-6 Bessel Functions and Their Properties-I
Bessel's Equation by Free Academy
Taylor Series, Bessel, single Variable Calculus, Coursera.org
Ordinary Differential Equations Lecture 7—Bessel functions and the unit step function
Laplace transform of Bessel function order zero
Laplace transform: Integral over Bessel function is one
Orthogonal Properties of Bessel Function, Orthogonal Properties of Bessel Equation
External Links
Addition formulas for Bessel functions by John D. Cook
Relations between Bessel functions by John D. Cook
Bessel's functions of the second order - C.V. Coates
References
- 1895: Andrew Gray and G.B. Mathews: A Treatise on Bessel Functions ... (previous) ... (next): Ch. 2 $10$
- 1953: Arthur Erdélyi, Wilhelm Magnus, Fritz Oberhettinger and Francesco G. Tricomi: Higher Transcendental Functions Volume II ... (previous) ... (next): $\S 7.2.1 (2)$
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $9.1.10$