Difference between revisions of "Shi"
From specialfunctionswiki
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
The hyperbolic sine integral is defined by the formula | The hyperbolic sine integral is defined by the formula | ||
| − | $$\mathrm{Shi}(z)=\displaystyle\int_0^z \dfrac{\mathrm{sinh}(t)}{t} | + | $$\mathrm{Shi}(z)=\displaystyle\int_0^z \dfrac{\mathrm{sinh}(t)}{t} \mathrm{d}t.$$ |
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
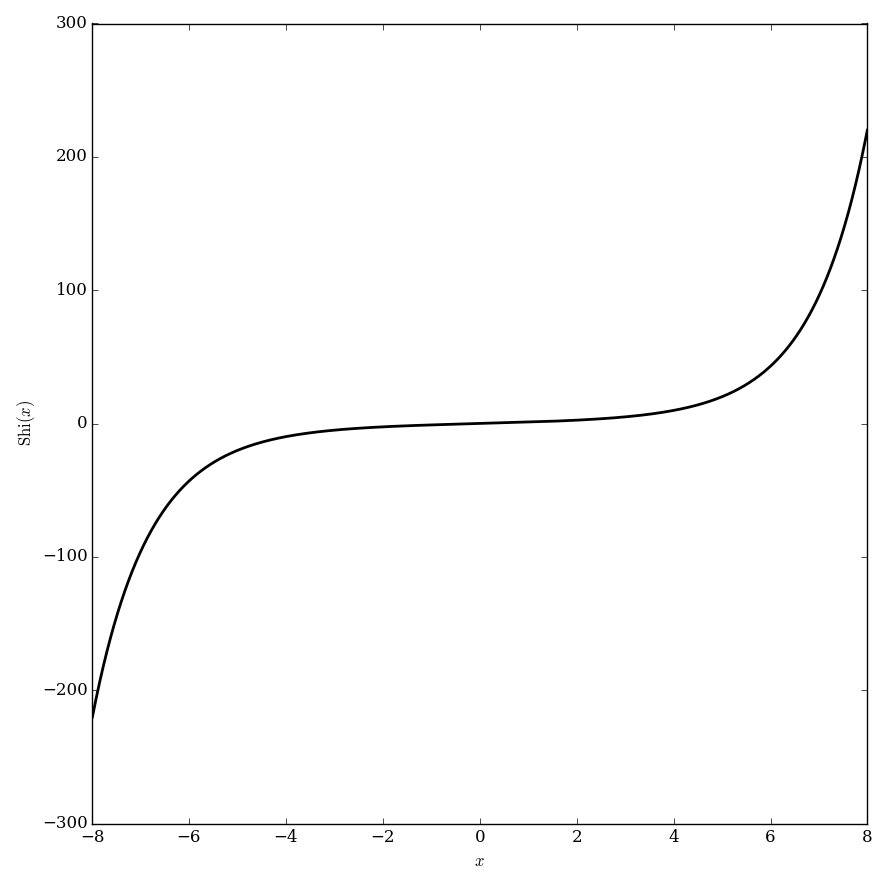
| − | File: | + | File:Shiplot.png|Plot of $\mathrm{Shi}$. |
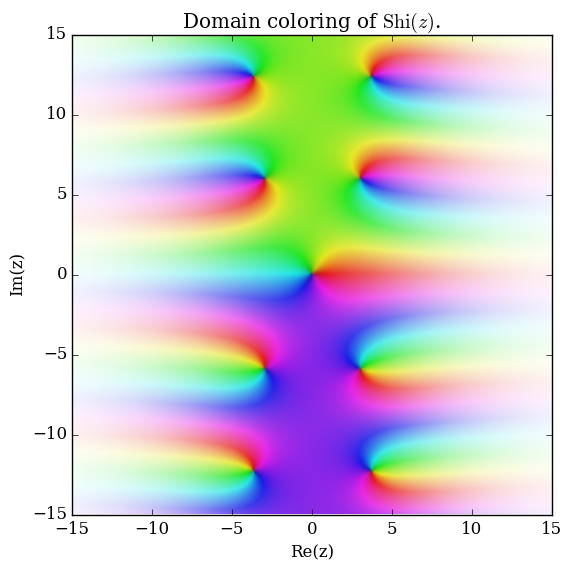
| − | File: | + | File:Complexshiplot.png|[[Domain coloring]] of $\mathrm{Shi}$. |
</gallery> | </gallery> | ||
</div> | </div> | ||
| − | + | {{:*-integral functions footer}} | |
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 23:11, 11 June 2016
The hyperbolic sine integral is defined by the formula $$\mathrm{Shi}(z)=\displaystyle\int_0^z \dfrac{\mathrm{sinh}(t)}{t} \mathrm{d}t.$$
Plot of $\mathrm{Shi}$.
Domain coloring of $\mathrm{Shi}$.
