Difference between revisions of "Inverse Gudermannian"
From specialfunctionswiki
| (5 intermediate revisions by the same user not shown) | |||
| Line 11: | Line 11: | ||
=Properties= | =Properties= | ||
| − | + | [[Relationship between sinh, inverse Gudermannian, and tan]]<br /> | |
| − | + | [[Relationship between cosh, inverse Gudermannian, and sec]]<br /> | |
| − | + | [[Relationship between tanh, inverse Gudermannian, and sin]]<br /> | |
| − | + | [[Relationship between csch, inverse Gudermannian, and cot]]<br /> | |
| − | + | [[Relationship between sech, inverse Gudermannian, and cos]]<br /> | |
| − | + | [[Relationship between coth, inverse Gudermannian, and csc]]<br /> | |
| − | + | {{:*-integral functions footer}} | |
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 23:10, 11 June 2016
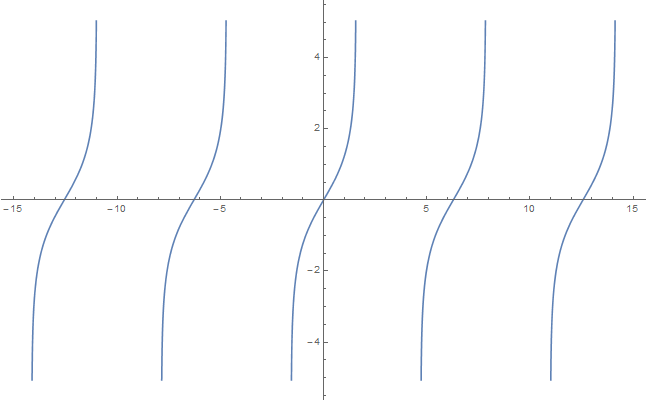
The inverse Gudermannian $\mathrm{gd}^{-1}$ is the inverse function of the Gudermannian function. It may be defined by the following formula for $x \in \mathbb{R}$: $$\mathrm{gd}^{-1}(x)=\displaystyle\int_0^x \dfrac{1}{\cosh(t)} dt,$$ where $\cosh$ denotes the hyperbolic cosine.
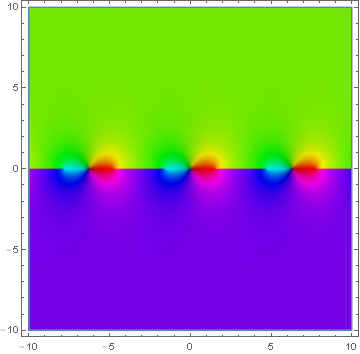
Domain coloring of $\mathrm{gd}^{-1}$.
Properties
Relationship between sinh, inverse Gudermannian, and tan
Relationship between cosh, inverse Gudermannian, and sec
Relationship between tanh, inverse Gudermannian, and sin
Relationship between csch, inverse Gudermannian, and cot
Relationship between sech, inverse Gudermannian, and cos
Relationship between coth, inverse Gudermannian, and csc