|
|
| (7 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| − | There are two functions commonly called $\mathrm{arccot}$, which refers to inverse functions of the [[cotangent | $\mathrm{cot}$]] function. First is the function $\mathrm{arccot_1}\colon \mathbb{R} \rightarrow (0,\pi)$ which results from restricting cotangent to $(0,\pi)$ and second is the function $\mathrm{arccot_2} \colon \mathbb{R} \rightarrow \left( -\frac{\pi}{2}, \frac{\pi}{2} \right) \setminus \{0\}$ which results from restricting cotangent to $\left( -\frac{\pi}{2}, \frac{\pi}{2} \right)$.
| + | __NOTOC__ |
| | + | The [[function]] $\mathrm{arccot} \colon \mathbb{R} \rightarrow \left( - \dfrac{\pi}{2}, \dfrac{\pi}{2} \right] \setminus \{0\}$ is the [[inverse function]] of the [[cotangent]] function. |
| | | | |
| | <div align="center"> | | <div align="center"> |
| | <gallery> | | <gallery> |
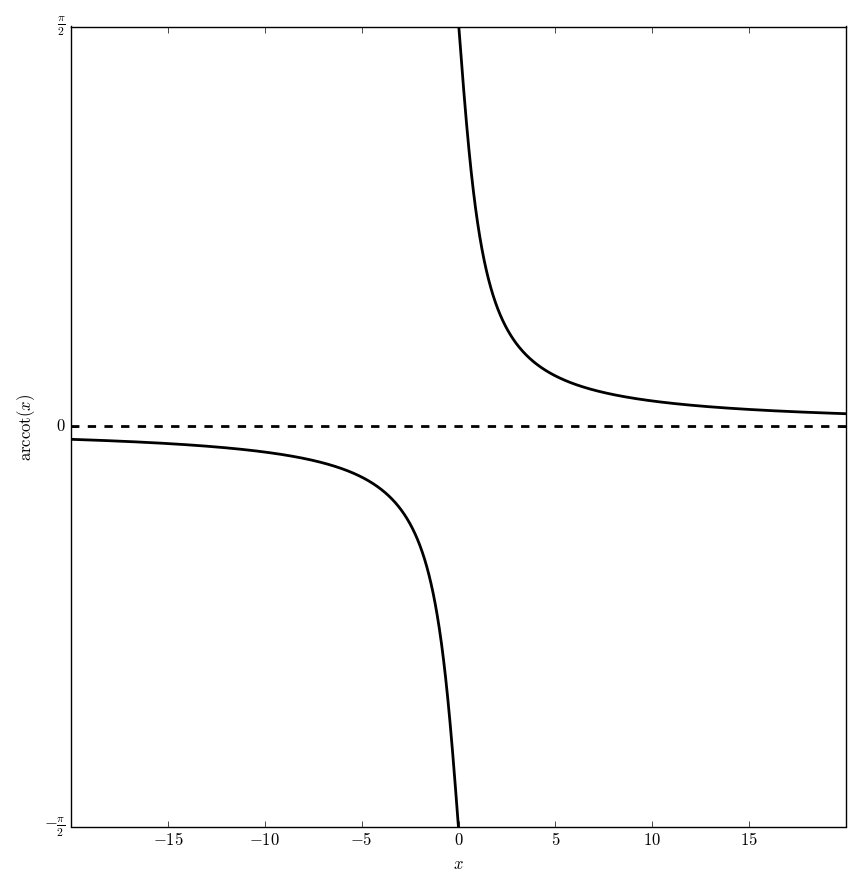
| − | File:Arccots.png|Graph of $\mathrm{arccot}_1$ and $\mathrm{arccot}_2$ on $\mathbb{R}$. | + | File:Arccotplot.png|Graph of $\mathrm{arccot}$ on $\mathbb{R}$. |
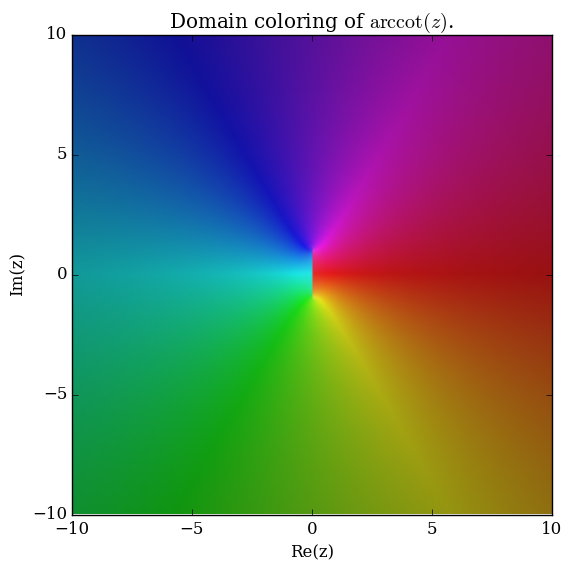
| − | File:Complex ArcCot.jpg|[[Domain coloring]] of [[analytic continuation]] $\mathrm{arccot}$. | + | File:Complexarccotplot.png|[[Domain coloring]] of $\mathrm{arccot}$. |
| | </gallery> | | </gallery> |
| | </div> | | </div> |
| | | | |
| | =Properties= | | =Properties= |
| − | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px">
| + | [[Derivative of arccot]] |
| − | <strong>Proposition:</strong>
| |
| − | $$\dfrac{d}{dz} \mathrm{arccot}(z) = -\dfrac{1}{z^2+1}$$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> If $y=\mathrm{arccot}(z)$ then $\cot(y)=z$. Now use [[implicit differentiation]] with respect to $z$ to get
| |
| − | $$-\csc^2(y)y'=1.$$
| |
| − | Substituting back in $y=\mathrm{arccos}(z)$ yields the formula
| |
| − | $$\dfrac{d}{dz} \mathrm{arccot}(z) = -\dfrac{1}{\csc^2(\mathrm{arccot}(z))} = -\dfrac{1}{z^2+1}.█$$
| |
| − | </div>
| |
| − | </div>
| |
| | | | |
| | =References= | | =References= |
| Line 28: |
Line 20: |
| | [[Arccoth]] | | [[Arccoth]] |
| | | | |
| − | <center>{{:Inverse trigonometric functions footer}}</center>
| + | {{:Inverse trigonometric functions footer}} |
| | + | |
| | + | [[Category:SpecialFunction]] |
Latest revision as of 03:44, 6 July 2016
The function $\mathrm{arccot} \colon \mathbb{R} \rightarrow \left( - \dfrac{\pi}{2}, \dfrac{\pi}{2} \right] \setminus \{0\}$ is the inverse function of the cotangent function.
Graph of $\mathrm{arccot}$ on $\mathbb{R}$.
Properties
Derivative of arccot
References
Which is the correct graph of arccot x?
See Also
Cotangent
Coth
Arccoth
Inverse trigonometric functions
Arccot