Difference between revisions of "Exponential"
| (20 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
| + | |||
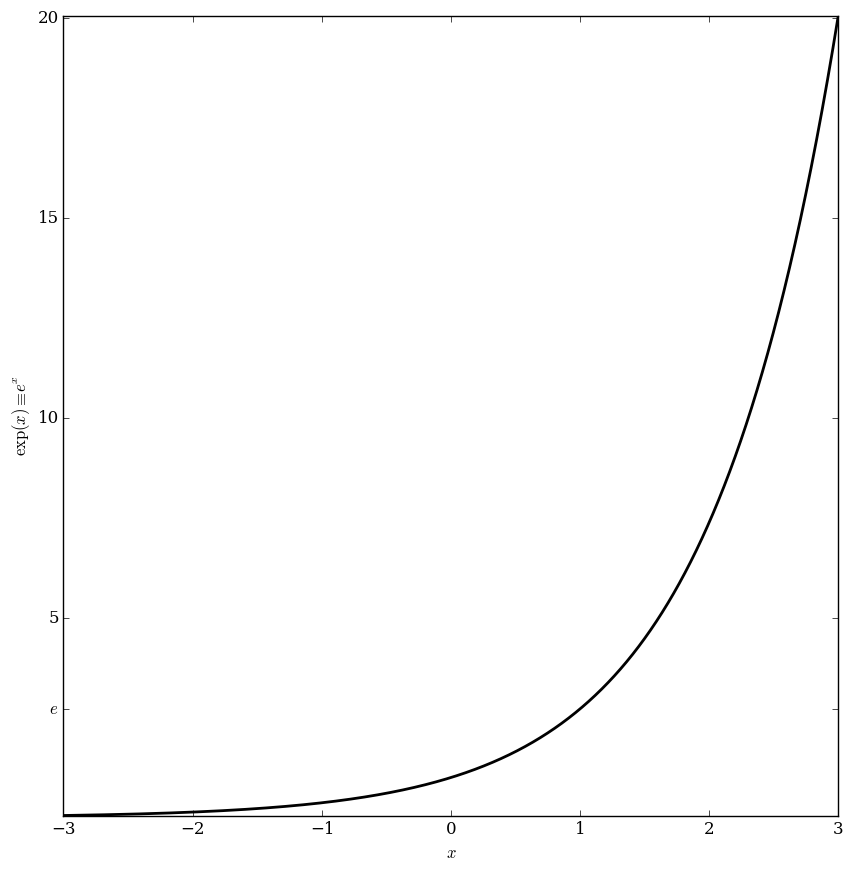
The exponential function $\exp \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by the formula | The exponential function $\exp \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by the formula | ||
| − | $$\exp(z) | + | $$\exp(z) \equiv e^z = \sum_{k=0}^{\infty} \dfrac{z^k}{k!},$$ |
| − | where $e$ is the [[E | base of the natural logarithm]]. | + | where $e$ is the [[E | base of the natural logarithm]]. |
| − | |||
| − | |||
| − | |||
| − | |||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
| − | File: | + | File:Exponentialplot.png|Graph of $\exp$. |
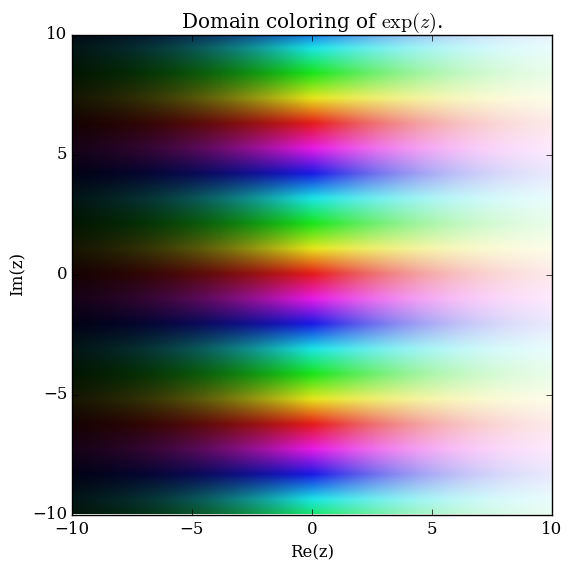
| − | File: | + | File:Complexexponentialplot.png|[[Domain coloring]] of $\exp$. |
</gallery> | </gallery> | ||
</div> | </div> | ||
=Properties= | =Properties= | ||
| − | + | [[Derivative of the exponential function]]<br /> | |
| − | + | [[Taylor series of the exponential function]]<br /> | |
| − | + | [[Euler E generating function]]<br /> | |
| + | [[Continued fraction for 1/sqrt(pi) integral from -infinity to infinity of e^(-t^2)/(z-t) dt]]<br /> | ||
| + | [[Exponential function is periodic with period 2pii]]<br /> | ||
| + | [[Euler's formula]]<br /> | ||
| + | [[E^(-x/(1-x)) is less than 1-x is less than e^(-x) for nonzero real x less than 1]]<br /> | ||
| + | [[E^x is greater than 1+x for nonzero real x]]<br /> | ||
| + | [[E^x is less than 1/(1-x) for nonzero real x less than 1]]<br /> | ||
| + | [[X/(1+x) less than 1-e^(-x) less than x for nonzero real x greater than -1]]<br /> | ||
| + | [[X less than e^x-1 less than x/(1-x) for nonzero real x less than 1]]<br /> | ||
| + | [[1+x greater than exp(x/(1+x)) for nonzero real x greater than -1]]<br /> | ||
| + | [[E^x greater than 1+x^n/n! for n greater than 0 and nonzero real x greater than 0]]<br /> | ||
| + | [[E^x greater than (1+x/y)^y greater than exp(xy/(x+y) for x greater than 0 and y greater than 0)]]<br /> | ||
| + | [[E^(-x) less than 1-(x/2) for 0 less than x less than or equal to 1.5936]]<br /> | ||
| + | [[Abs(z)/4 less than abs(e^z-1) less than (7abs(z))/4 for 0 less than abs(z) less than 1]]<br /> | ||
| + | [[Abs(e^z-1) less than or equal to e^(abs(z))-1 less than or equal to abs(z)e^(abs(z))]]<br /> | ||
| + | [[Sum of cosh and sinh]]<br /> | ||
| + | [[Difference of cosh and sinh]]<br /> | ||
| + | |||
| + | ==References== | ||
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Logarithm (multivalued) of the exponential}}: $4.2.1$ | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
| + | [[Category:Definition]] | ||
Latest revision as of 23:37, 21 October 2017
The exponential function $\exp \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by the formula
$$\exp(z) \equiv e^z = \sum_{k=0}^{\infty} \dfrac{z^k}{k!},$$
where $e$ is the base of the natural logarithm.
Domain coloring of $\exp$.
Properties
Derivative of the exponential function
Taylor series of the exponential function
Euler E generating function
Continued fraction for 1/sqrt(pi) integral from -infinity to infinity of e^(-t^2)/(z-t) dt
Exponential function is periodic with period 2pii
Euler's formula
E^(-x/(1-x)) is less than 1-x is less than e^(-x) for nonzero real x less than 1
E^x is greater than 1+x for nonzero real x
E^x is less than 1/(1-x) for nonzero real x less than 1
X/(1+x) less than 1-e^(-x) less than x for nonzero real x greater than -1
X less than e^x-1 less than x/(1-x) for nonzero real x less than 1
1+x greater than exp(x/(1+x)) for nonzero real x greater than -1
E^x greater than 1+x^n/n! for n greater than 0 and nonzero real x greater than 0
E^x greater than (1+x/y)^y greater than exp(xy/(x+y) for x greater than 0 and y greater than 0)
E^(-x) less than 1-(x/2) for 0 less than x less than or equal to 1.5936
Abs(z)/4 less than abs(e^z-1) less than (7abs(z))/4 for 0 less than abs(z) less than 1
Abs(e^z-1) less than or equal to e^(abs(z))-1 less than or equal to abs(z)e^(abs(z))
Sum of cosh and sinh
Difference of cosh and sinh
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.2.1$