Difference between revisions of "Spherical Bessel y"
From specialfunctionswiki
m (Tom moved page Spherical Bessel y sub nu to Spherical Bessel y) |
|||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
The spherical Bessel function of the second kind is | The spherical Bessel function of the second kind is | ||
$$y_{\nu}(z)=\sqrt{\dfrac{\pi}{2z}} Y_{\nu+\frac{1}{2}}(z),$$ | $$y_{\nu}(z)=\sqrt{\dfrac{\pi}{2z}} Y_{\nu+\frac{1}{2}}(z),$$ | ||
| Line 10: | Line 11: | ||
=Properties= | =Properties= | ||
| − | + | [[Relationship between spherical Bessel y and cosine]] | |
| − | + | =References= | |
| + | |||
| + | {{:Bessel functions footer}} | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 01:14, 18 July 2016
The spherical Bessel function of the second kind is $$y_{\nu}(z)=\sqrt{\dfrac{\pi}{2z}} Y_{\nu+\frac{1}{2}}(z),$$ where $Y_{\nu}$ denotes the Bessel function of the second kind.
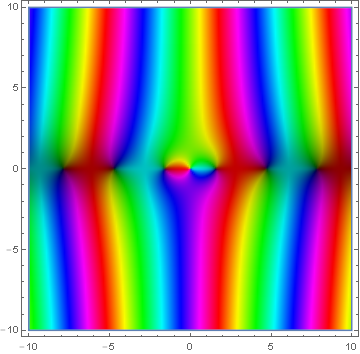
Domain coloring of $y_0$.
Properties
Relationship between spherical Bessel y and cosine
References
Spherical Bessel $y_{\nu}$