Difference between revisions of "Gudermannian"
From specialfunctionswiki
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
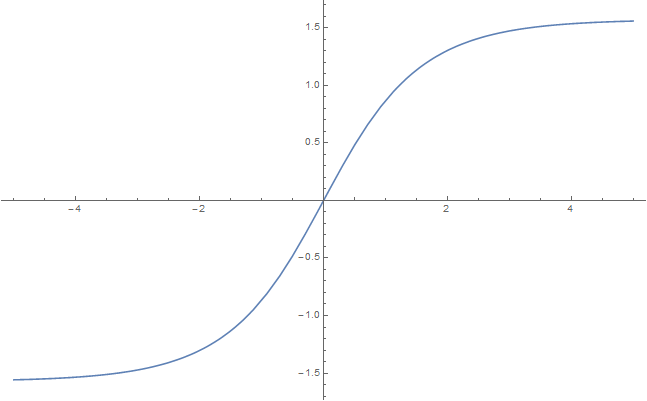
The Gudermannian $\mathrm{gd}$ is defined for $x \in \mathbb{R}$ by the formula | The Gudermannian $\mathrm{gd}$ is defined for $x \in \mathbb{R}$ by the formula | ||
| − | $$\mathrm{gd}(x) = \displaystyle\int_0^x \ | + | $$\mathrm{gd}(x) = \displaystyle\int_0^x \mathrm{sech}(t) \mathrm{d}t,$$ |
| + | where $\mathrm{sech}$ denotes the [[sech|hyperbolic secant]]. | ||
<div align="center"> | <div align="center"> | ||
| Line 10: | Line 11: | ||
=Properties= | =Properties= | ||
| − | + | [[Derivative of Gudermannian]]<br /> | |
| − | + | [[Taylor series for Gudermannian]]<br /> | |
| − | + | [[Relationship between sine, Gudermannian, and tanh]]<br /> | |
| − | + | [[Relationship between cosine, Gudermannian, and sech]]<br /> | |
| − | + | [[Relationship between tangent, Gudermannian, and sinh]]<br /> | |
| − | + | [[Relationship between csc, Gudermannian, and coth]]<br /> | |
| − | + | [[Relationship between secant, Gudermannian, and cosh]]<br /> | |
| − | + | [[Relationship between cot, Gudermannian, and csch]]<br /> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {{:*-integral functions footer}} | ||
| − | + | [[Category:SpecialFunction]] | |
Latest revision as of 22:07, 19 September 2016
The Gudermannian $\mathrm{gd}$ is defined for $x \in \mathbb{R}$ by the formula $$\mathrm{gd}(x) = \displaystyle\int_0^x \mathrm{sech}(t) \mathrm{d}t,$$ where $\mathrm{sech}$ denotes the hyperbolic secant.
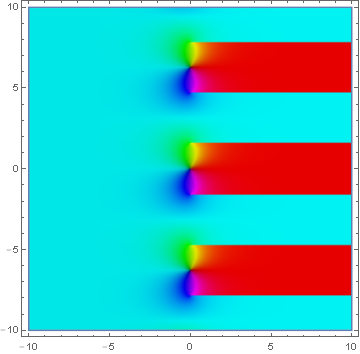
Domain coloring of $\mathrm{gd}$.
Properties
Derivative of Gudermannian
Taylor series for Gudermannian
Relationship between sine, Gudermannian, and tanh
Relationship between cosine, Gudermannian, and sech
Relationship between tangent, Gudermannian, and sinh
Relationship between csc, Gudermannian, and coth
Relationship between secant, Gudermannian, and cosh
Relationship between cot, Gudermannian, and csch