Difference between revisions of "Dirichlet eta"
From specialfunctionswiki
(s -> z) |
|||
| (4 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
Let $\mathrm{Re} \hspace{2pt} z > 0$, then define | Let $\mathrm{Re} \hspace{2pt} z > 0$, then define | ||
| − | $$\eta(z) = \displaystyle\sum_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{n^ | + | $$\eta(z) = \displaystyle\sum_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{n^z}.$$ |
| − | |||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
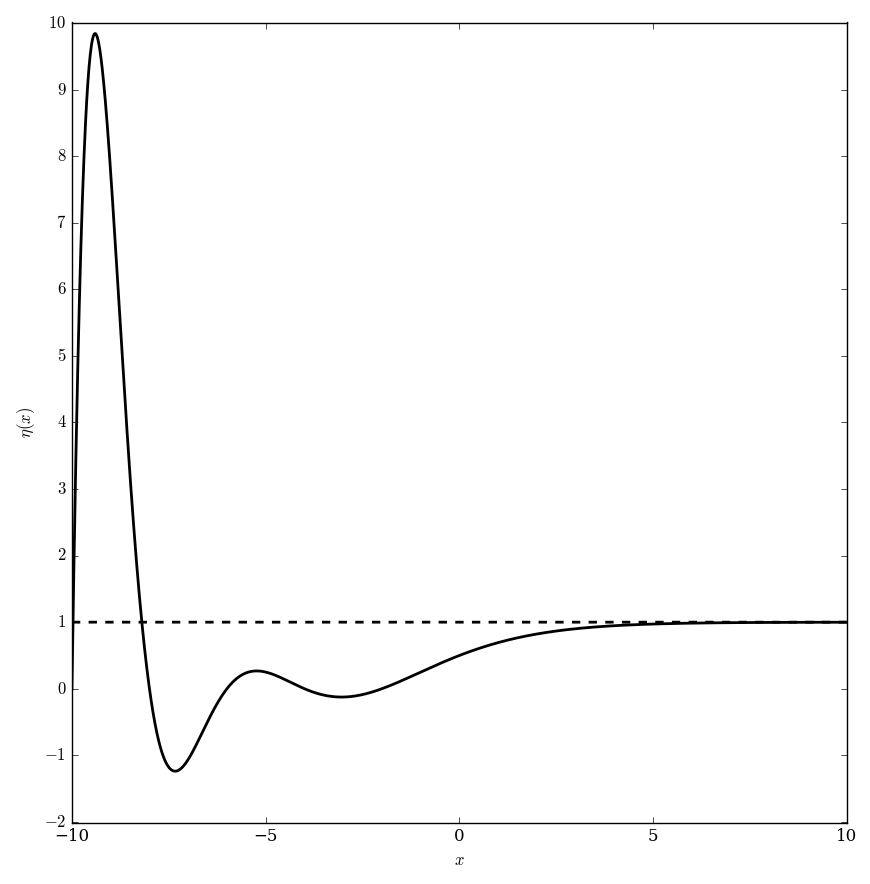
| − | File: | + | File:Dirichletetaplot.png|Graph of $\eta$. |
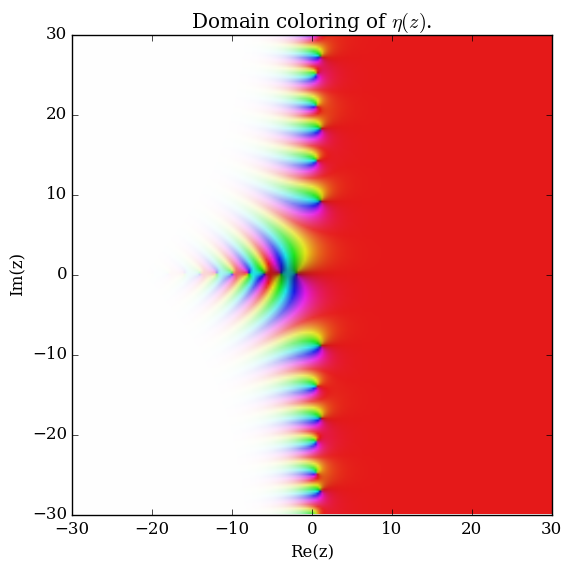
| + | File:Complexdirichletetaplot.png|[[Domain coloring]] of $\eta$. | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| Line 11: | Line 11: | ||
=See Also= | =See Also= | ||
[[Riemann zeta]]<br /> | [[Riemann zeta]]<br /> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 20:58, 5 November 2017
Let $\mathrm{Re} \hspace{2pt} z > 0$, then define $$\eta(z) = \displaystyle\sum_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{n^z}.$$
Domain coloring of $\eta$.