Difference between revisions of "Prime counting"
From specialfunctionswiki
| (2 intermediate revisions by the same user not shown) | |||
| Line 9: | Line 9: | ||
=Properties= | =Properties= | ||
| − | + | [[Prime number theorem, pi and x/log(x)]]<br /> | |
| − | + | [[Prime number theorem, logarithmic integral]]<br /> | |
=References= | =References= | ||
| Line 16: | Line 16: | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
| + | |||
| + | {{:Number theory functions footer}} | ||
Latest revision as of 06:35, 22 June 2016
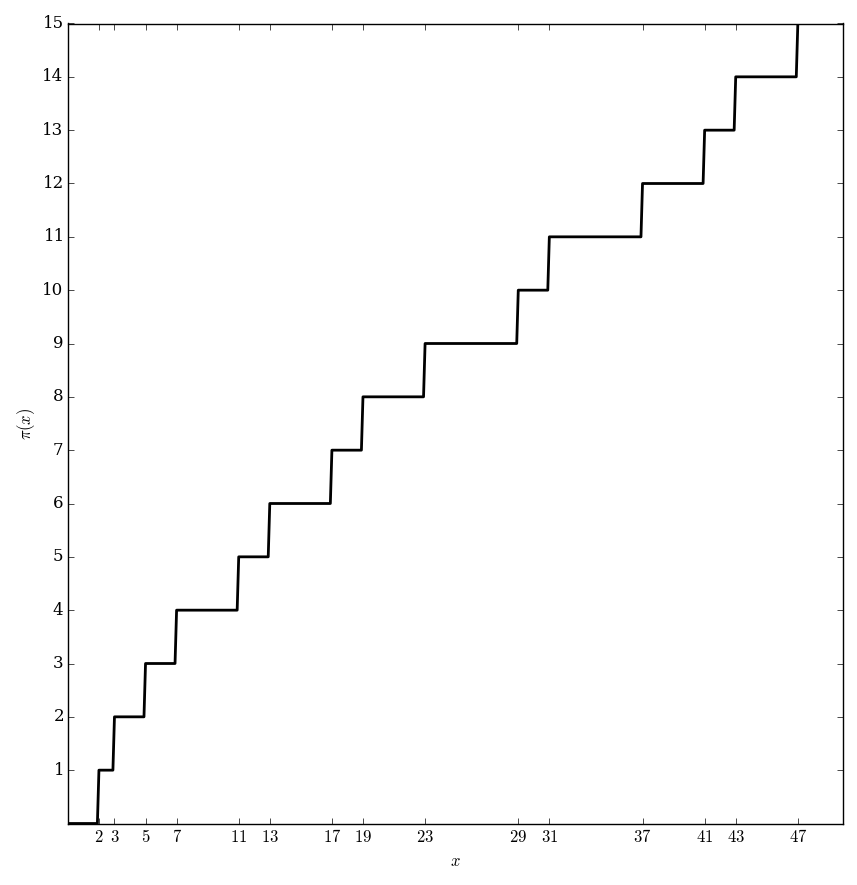
The prime counting function $\pi \colon \mathbb{R} \rightarrow \mathbb{Z}^+$ is defined by the formula $$\pi(x) = \{\mathrm{number \hspace{2pt} of \hspace{2pt} primes} \leq x \}.$$
Properties
Prime number theorem, pi and x/log(x)
Prime number theorem, logarithmic integral
References
Newman's short proof of the prime number theorem