Difference between revisions of "Secant"
From specialfunctionswiki
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
| + | |||
The secant function is defined by | The secant function is defined by | ||
| − | $$\sec(z)=\dfrac{1}{\cos(z)} | + | $$\sec(z)=\dfrac{1}{\cos(z)},$$ |
| + | where $\cos$ denotes the [[cosine]]. | ||
<div align="center"> | <div align="center"> | ||
| Line 6: | Line 9: | ||
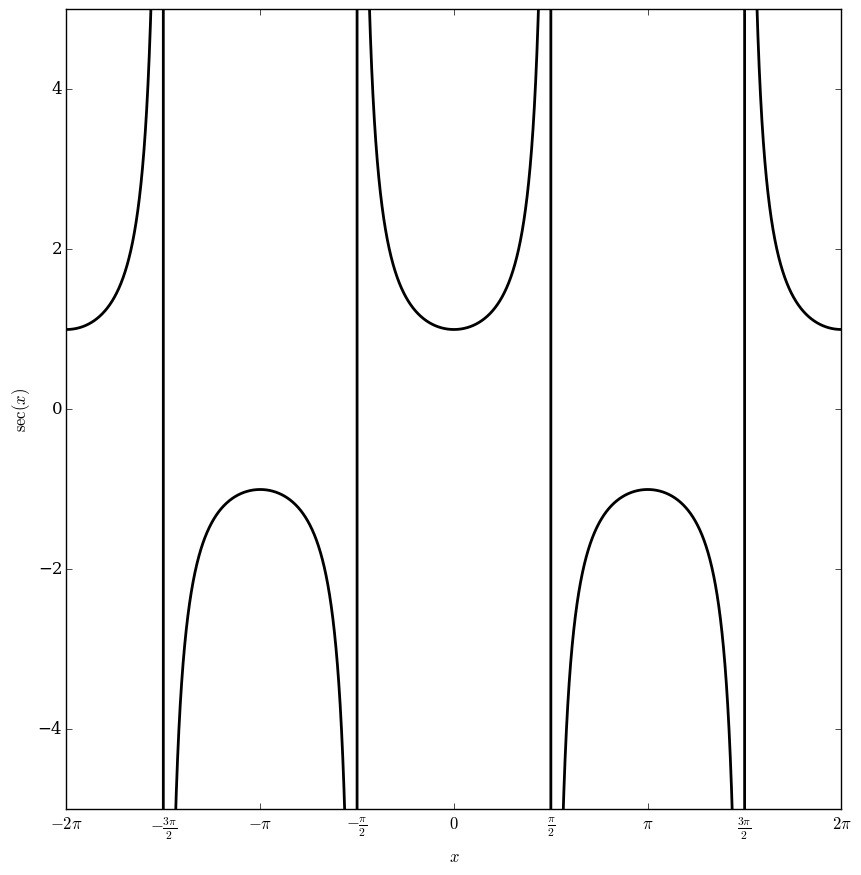
File:Secantplot.png|Graph of $\sec$ over $[-2\pi,2\pi]$. | File:Secantplot.png|Graph of $\sec$ over $[-2\pi,2\pi]$. | ||
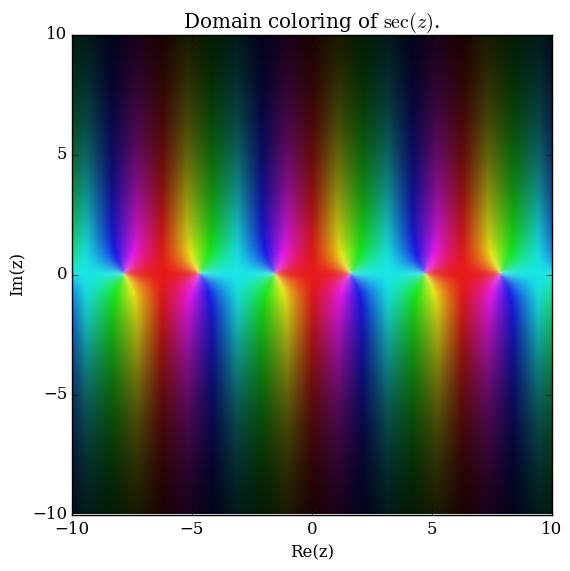
File:Complexsecantplot.png|[[Domain coloring]] of $\sec$. | File:Complexsecantplot.png|[[Domain coloring]] of $\sec$. | ||
| + | File:Trig Functions Diagram.svg|Trig functions diagram using the unit circle. | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
=Properties= | =Properties= | ||
| − | + | [[Derivative of secant]]<br /> | |
| − | + | [[Relationship between secant, Gudermannian, and cosh]]<br /> | |
| − | + | [[Relationship between cosh, inverse Gudermannian, and sec]]<br /> | |
=See Also= | =See Also= | ||
| Line 20: | Line 24: | ||
=References= | =References= | ||
| − | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev= | + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Cosecant|next=Cotangent}}: 4.3.5 |
| − | + | {{:Trigonometric functions footer}} | |
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 20:45, 26 February 2017
The secant function is defined by
$$\sec(z)=\dfrac{1}{\cos(z)},$$
where $\cos$ denotes the cosine.
Graph of $\sec$ over $[-2\pi,2\pi]$.
Domain coloring of $\sec$.
Trig functions diagram using the unit circle.
Properties
Derivative of secant
Relationship between secant, Gudermannian, and cosh
Relationship between cosh, inverse Gudermannian, and sec
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 4.3.5
