Difference between revisions of "Exsecant"
From specialfunctionswiki
(Created page with "The exsecant function $\mathrm{exsec}$ is defined by $$\mathrm{exsec}(z)=\sec(z)-1,$$ where $\sec$ denotes the secant. =Properties= =References= * {{BookReference|Handbo...") |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
$$\mathrm{exsec}(z)=\sec(z)-1,$$ | $$\mathrm{exsec}(z)=\sec(z)-1,$$ | ||
where $\sec$ denotes the [[secant]]. | where $\sec$ denotes the [[secant]]. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
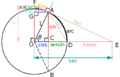
| + | File:Trig Functions Diagram.svg|Trig functions diagram using the unit circle. | ||
| + | </gallery> | ||
| + | </div> | ||
=Properties= | =Properties= | ||
| + | [[Derivative of exsecant]] <br /> | ||
| + | [[Antiderivative of exsecant]] <br /> | ||
=References= | =References= | ||
| − | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Haversine|next=Law of Sines}}: 4.3.147 | + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Haversine|next=Law of Sines}}: $4.3.147$ |
| − | [[Category: | + | [[Category:SpecialFunction]] |
| + | [[Category:Definition]] | ||
Latest revision as of 04:11, 28 March 2017
The exsecant function $\mathrm{exsec}$ is defined by $$\mathrm{exsec}(z)=\sec(z)-1,$$ where $\sec$ denotes the secant.
Trig functions diagram using the unit circle.
Properties
Derivative of exsecant
Antiderivative of exsecant
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.3.147$
