Difference between revisions of "Secant"
From specialfunctionswiki
| (One intermediate revision by the same user not shown) | |||
| Line 2: | Line 2: | ||
The secant function is defined by | The secant function is defined by | ||
| − | $$\sec(z)=\dfrac{1}{\cos(z)} | + | $$\sec(z)=\dfrac{1}{\cos(z)},$$ |
| + | where $\cos$ denotes the [[cosine]]. | ||
<div align="center"> | <div align="center"> | ||
| Line 25: | Line 26: | ||
* {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Cosecant|next=Cotangent}}: 4.3.5 | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Cosecant|next=Cotangent}}: 4.3.5 | ||
| − | + | {{:Trigonometric functions footer}} | |
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 20:45, 26 February 2017
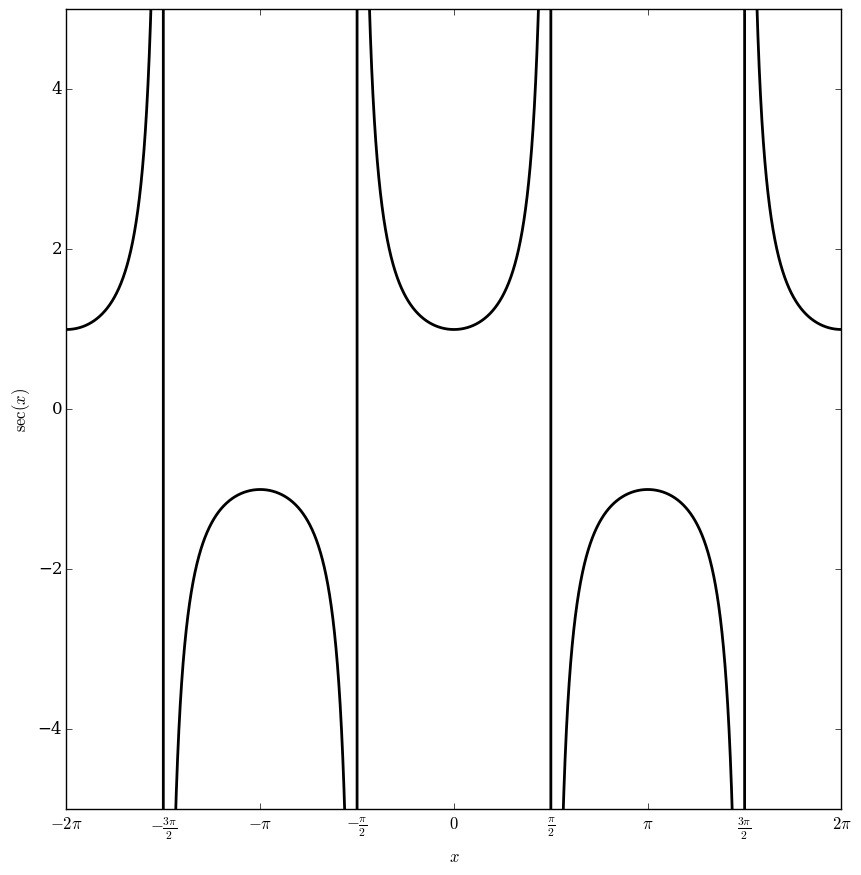
The secant function is defined by
$$\sec(z)=\dfrac{1}{\cos(z)},$$
where $\cos$ denotes the cosine.
Graph of $\sec$ over $[-2\pi,2\pi]$.
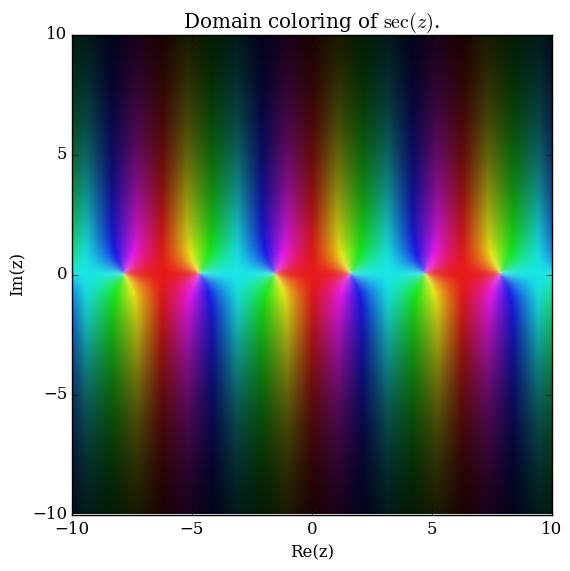
Domain coloring of $\sec$.
Trig functions diagram using the unit circle.
Properties
Derivative of secant
Relationship between secant, Gudermannian, and cosh
Relationship between cosh, inverse Gudermannian, and sec
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 4.3.5
