Difference between revisions of "Bessel Y"
From specialfunctionswiki
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Bessel functions of the second kind $Y_{\nu}$ are defined via the formula | + | Bessel functions of the second kind, $Y_{\nu}$, are defined via the formula |
$$Y_{\nu}(z)=\dfrac{J_{\nu}(z)\cos(\nu \pi)-J_{-\nu}(z)}{\sin(\nu \pi)}.$$ | $$Y_{\nu}(z)=\dfrac{J_{\nu}(z)\cos(\nu \pi)-J_{-\nu}(z)}{\sin(\nu \pi)}.$$ | ||
Sometimes these functions are called Neumann functions and have the notation $N_{\nu}$ instead of $Y_{\nu}$. | Sometimes these functions are called Neumann functions and have the notation $N_{\nu}$ instead of $Y_{\nu}$. | ||
| Line 16: | Line 16: | ||
=Properties= | =Properties= | ||
| − | + | [[Derivative of Bessel Y with respect to its order]] | |
=References= | =References= | ||
| − | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Hankel H (1)}}: 9.1. | + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Hankel H (1)}}: 9.1.2 |
[http://gdz.sub.uni-goettingen.de/dms/load/img/?PID=PPN600494829_0021%7CLOG_0023 Bessel's functions of the second order - C.V. Coates]<br /> | [http://gdz.sub.uni-goettingen.de/dms/load/img/?PID=PPN600494829_0021%7CLOG_0023 Bessel's functions of the second order - C.V. Coates]<br /> | ||
Latest revision as of 15:39, 10 July 2017
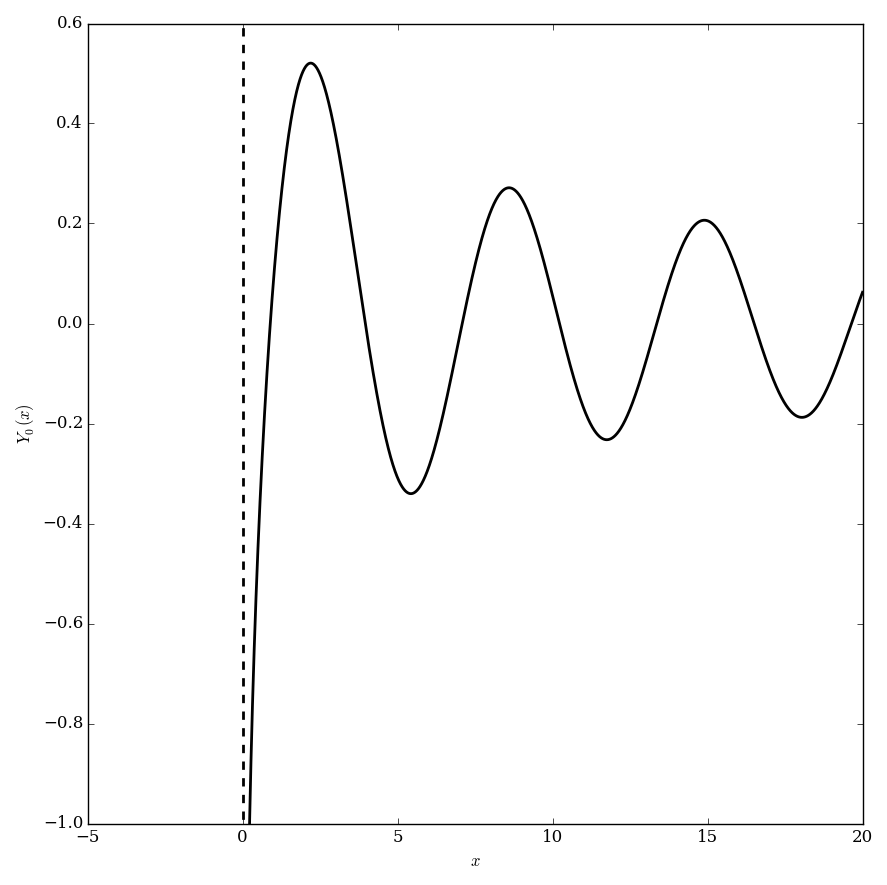
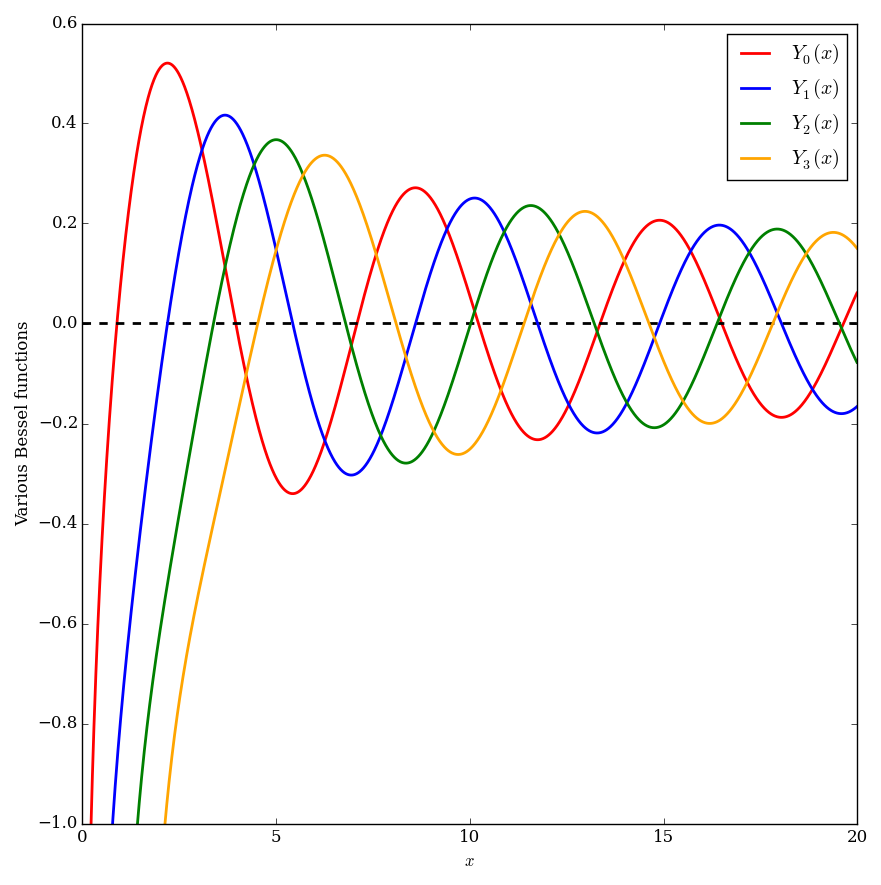
Bessel functions of the second kind, $Y_{\nu}$, are defined via the formula $$Y_{\nu}(z)=\dfrac{J_{\nu}(z)\cos(\nu \pi)-J_{-\nu}(z)}{\sin(\nu \pi)}.$$ Sometimes these functions are called Neumann functions and have the notation $N_{\nu}$ instead of $Y_{\nu}$.
Graph of $Y_0$.
Graph of $Y_0,Y_1,Y_2$, and $Y_3$.
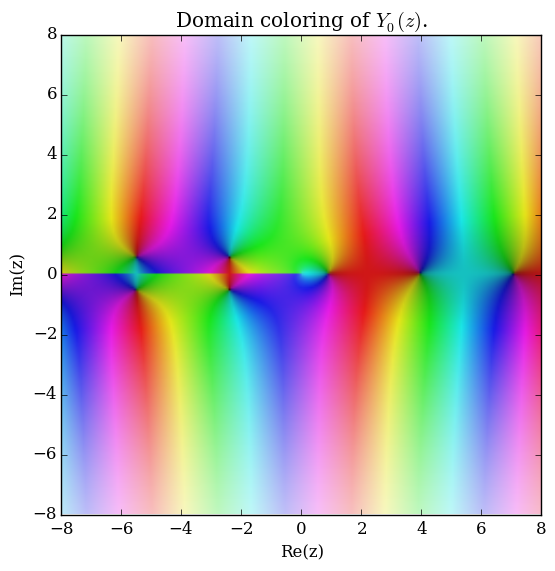
Domain coloring of $Y_0$.
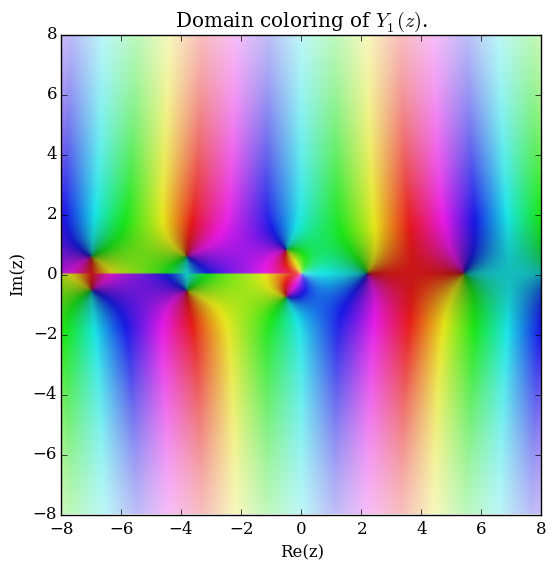
Domain coloring of $Y_1$.
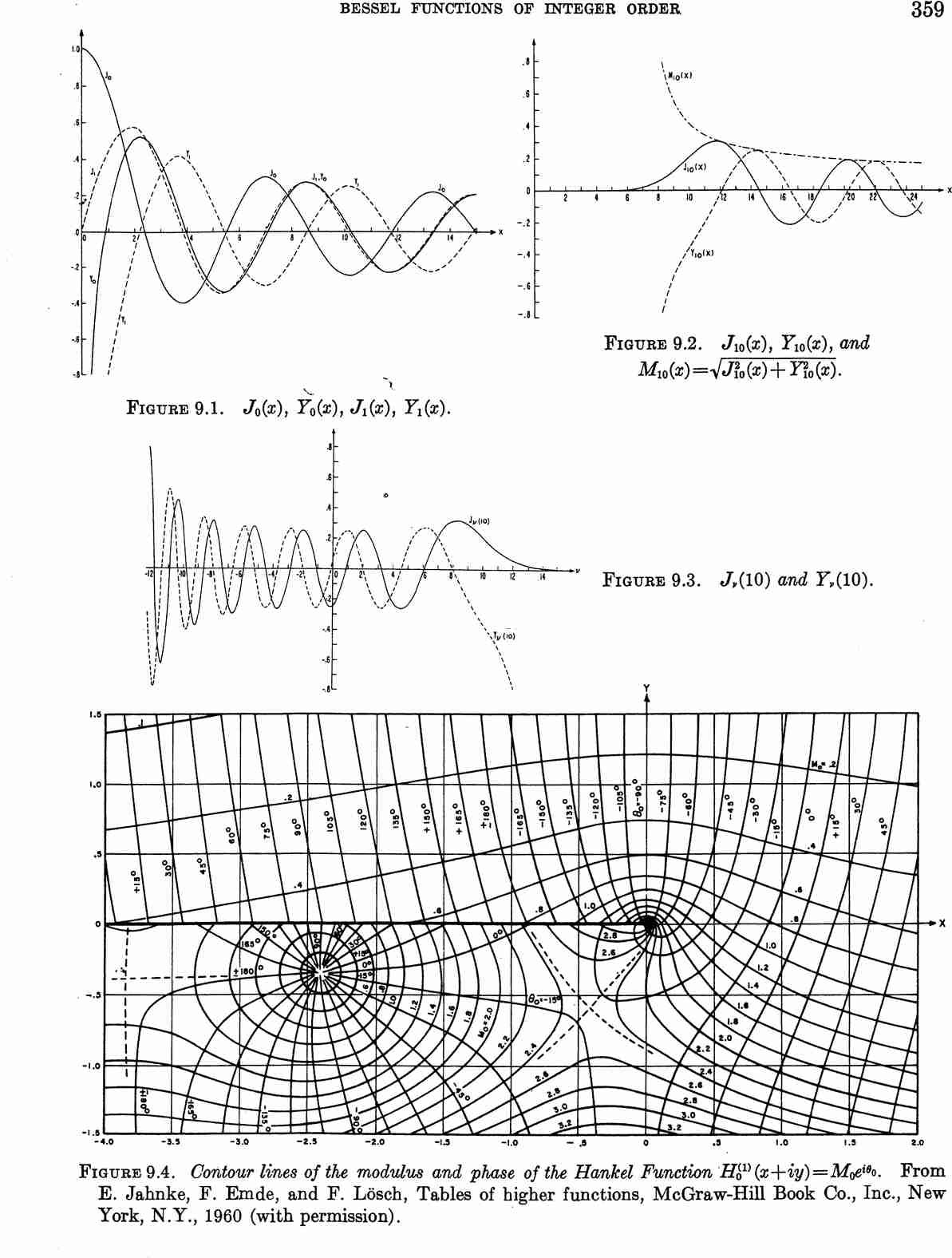
Bessel functions from Abramowitz&Stegun
.jpg)
Properties
Derivative of Bessel Y with respect to its order
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 9.1.2
Bessel's functions of the second order - C.V. Coates
