Difference between revisions of "Euler phi"
From specialfunctionswiki
| Line 13: | Line 13: | ||
=References= | =References= | ||
| + | |||
| + | {{:Number theory functions footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 06:33, 22 June 2016
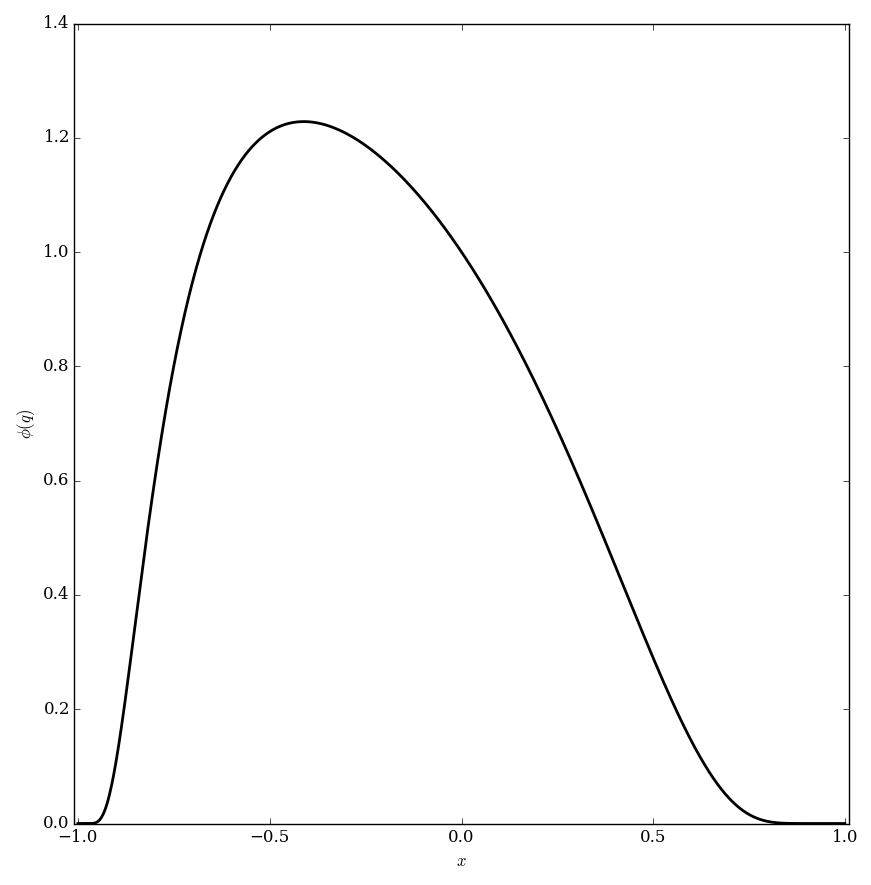
The Euler phi function (not to be confused with the Euler totient) is defined for $q \in \mathbb{C}$ with $|q|<1$ by $$\phi(q) = \displaystyle\prod_{k=1}^{\infty} 1-q^k.$$
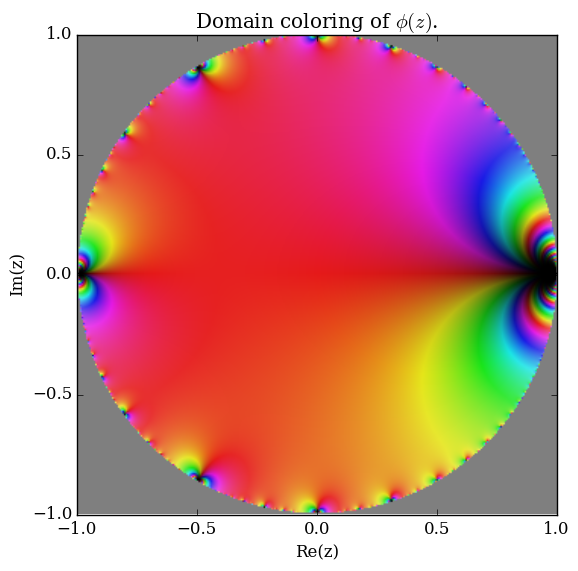
Domain coloring $\phi$.
Properties
Relationship between Euler phi and q-Pochhammer