Difference between revisions of "Secant"
From specialfunctionswiki
| Line 2: | Line 2: | ||
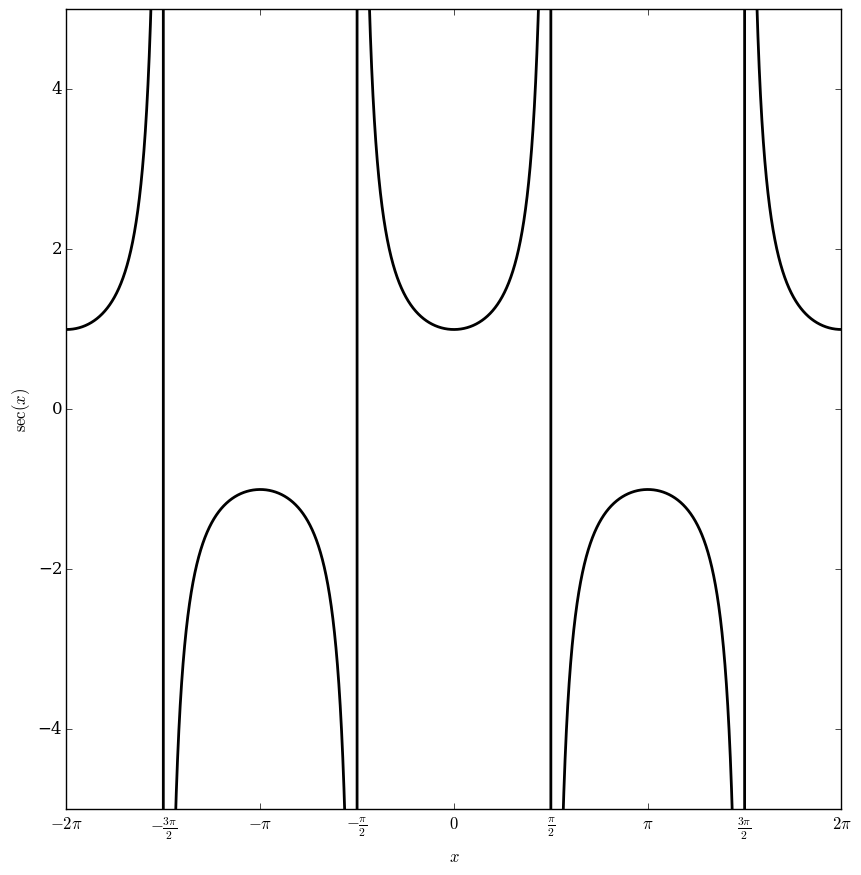
The secant function is defined by | The secant function is defined by | ||
| − | $$\sec(z)=\dfrac{1}{\cos(z)} | + | $$\sec(z)=\dfrac{1}{\cos(z)},$$ |
| + | where $\cos$ denotes the [[cosine]]. | ||
<div align="center"> | <div align="center"> | ||
Latest revision as of 20:45, 26 February 2017
The secant function is defined by
$$\sec(z)=\dfrac{1}{\cos(z)},$$
where $\cos$ denotes the cosine.
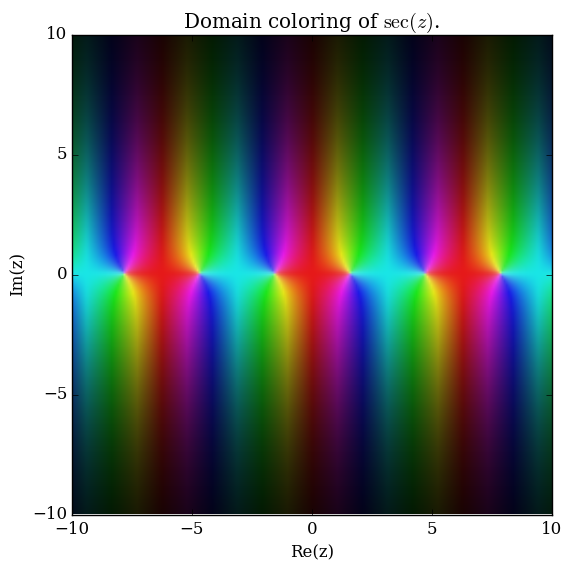
Domain coloring of $\sec$.
Properties
Derivative of secant
Relationship between secant, Gudermannian, and cosh
Relationship between cosh, inverse Gudermannian, and sec
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 4.3.5