Difference between revisions of "Arccosh"
From specialfunctionswiki
(→Properties) |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
The inverse hyperbolic cosine function $\mathrm{arccosh}$ is the [[inverse function]] of the [[hyperbolic cosine]] function. It may be defined by | The inverse hyperbolic cosine function $\mathrm{arccosh}$ is the [[inverse function]] of the [[hyperbolic cosine]] function. It may be defined by | ||
| − | $$\mathrm{arccosh}(z)=\log \left(z + \sqrt{1+z^2} \right) | + | $$\mathrm{arccosh}(z)=\log \left(z + \sqrt{1+z^2} \right),$$ |
| + | where $\log$ denotes the [[logarithm]]. | ||
<div align="center"> | <div align="center"> | ||
| Line 10: | Line 11: | ||
=Properties= | =Properties= | ||
| + | [[Derivative of arccosh]] <br /> | ||
| + | [[Antiderivative of arccosh]]<br /> | ||
=See Also= | =See Also= | ||
Latest revision as of 23:42, 11 December 2016
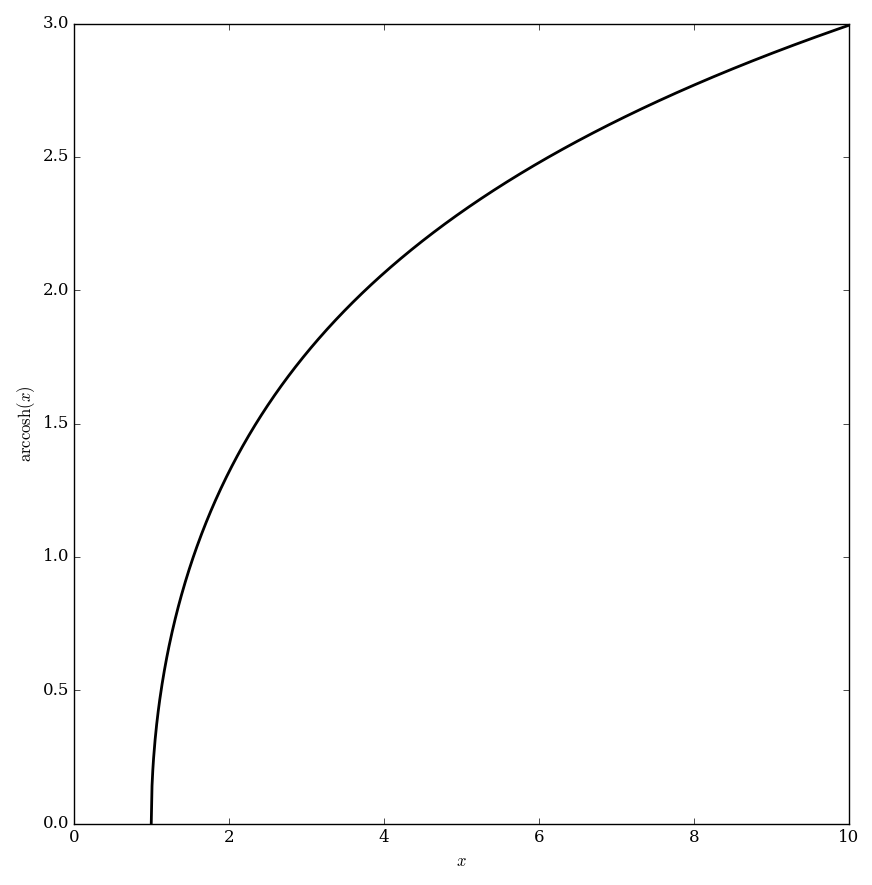
The inverse hyperbolic cosine function $\mathrm{arccosh}$ is the inverse function of the hyperbolic cosine function. It may be defined by $$\mathrm{arccosh}(z)=\log \left(z + \sqrt{1+z^2} \right),$$ where $\log$ denotes the logarithm.
Graph of $\mathrm{arccos}$ on $[1,10]$.
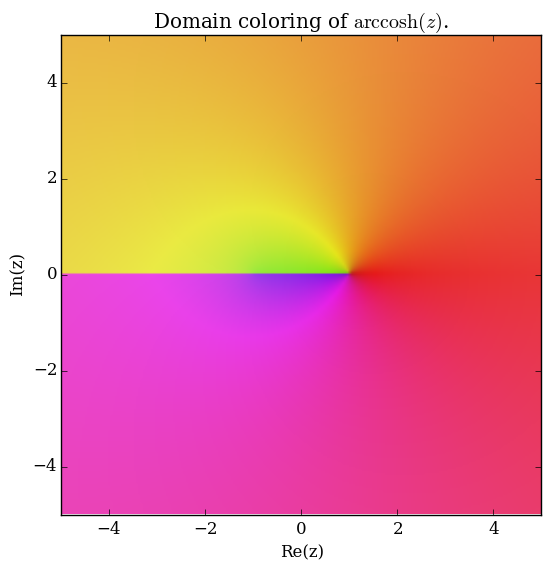
Domain coloring of $\mathrm{arccosh}$.
Properties
Derivative of arccosh
Antiderivative of arccosh
