Latest revision as of 04:56, 16 September 2016

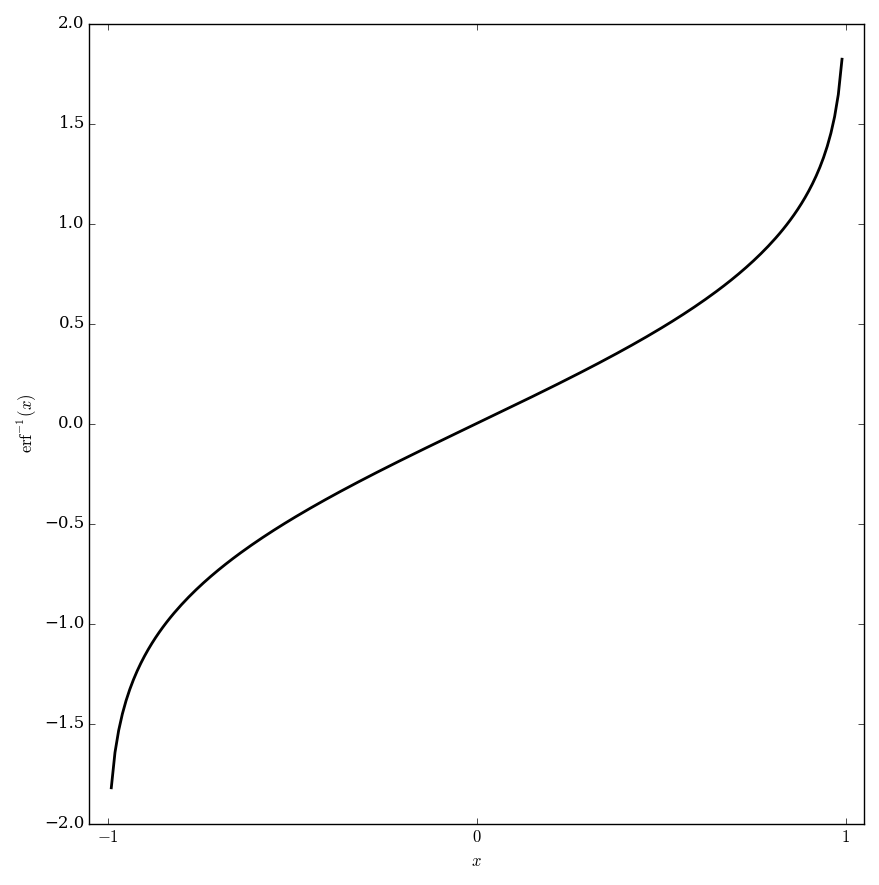
The inverse error function is the inverse function of the error function. We denote it by writing $\mathrm{erf}^{-1}$.

Properties

Error functions

Error function

Inverse $\mathrm{erf}$

@@ Line 10: / Line 10: @@
 [[Derivative of inverse error function]]<br />
 [[Antiderivative of inverse error function]]<br />
+[[Integral of inverse erf from 0 to 1]]<br />
+[[Integral of log of inverse erf from 0 to 1]]<br />
-<div class="toccolours mw-collapsible mw-collapsed">
+{{:Error functions footer}}
-<strong>Theorem:</strong> The following formula holds:
-$$\displaystyle\int_0^1 \mathrm{erf}^{-1}(x) dx=\dfrac{1}{\sqrt{\pi}}.$$
-<div class="mw-collapsible-content">
-<strong>Proof:</strong> █
-</div>
-</div>
-<div class="toccolours mw-collapsible mw-collapsed">
-<strong>Theorem:</strong> The following formula holds:
-$$\displaystyle\int_0^1 \log(\mathrm{erf}^{-1}(x)) dx = \left( \dfrac{\gamma}{2} + \log(2) \right),$$
-where $\mathrm{erf}^{-1}$ denotes the [[inverse error function]], $\log$ denotes the [[logarithm]], and $\gamma$ denotes the [[Euler-Mascheroni constant]].
-<div class="mw-collapsible-content">
-<strong>Proof:</strong> █
-</div>
-</div>
-<center>{{:Error functions footer}}</center>
 [[Category:SpecialFunction]]