Difference between revisions of "Fresnel S"
From specialfunctionswiki
(→Videos) |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 13: | Line 13: | ||
[[Fresnel S is odd]] <br /> | [[Fresnel S is odd]] <br /> | ||
[[Taylor series for Fresnel S]]<br /> | [[Taylor series for Fresnel S]]<br /> | ||
| − | + | [[Fresnel S in terms of erf]]<br /> | |
| − | [[Fresnel S in terms of | ||
[[Limiting value of Fresnel S]]<br /> | [[Limiting value of Fresnel S]]<br /> | ||
| − | |||
=See Also= | =See Also= | ||
| Line 22: | Line 20: | ||
=Videos= | =Videos= | ||
| − | [https://www.youtube.com/watch?v=fFZ6BsH99-0 The Fresnel Integral S(x) - How to integrate sin(x^2)]<br /> | + | [https://www.youtube.com/watch?v=fFZ6BsH99-0 The Fresnel Integral S(x) - How to integrate sin(x^2) (12 February 2015)]<br /> |
| − | + | [https://www.youtube.com/watch?v=H3uOq7VujYA Math and Physics: The Fresnel Integrals (12 May 2016)] <br /> | |
{{:*-integral functions footer}} | {{:*-integral functions footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 17:21, 5 October 2016
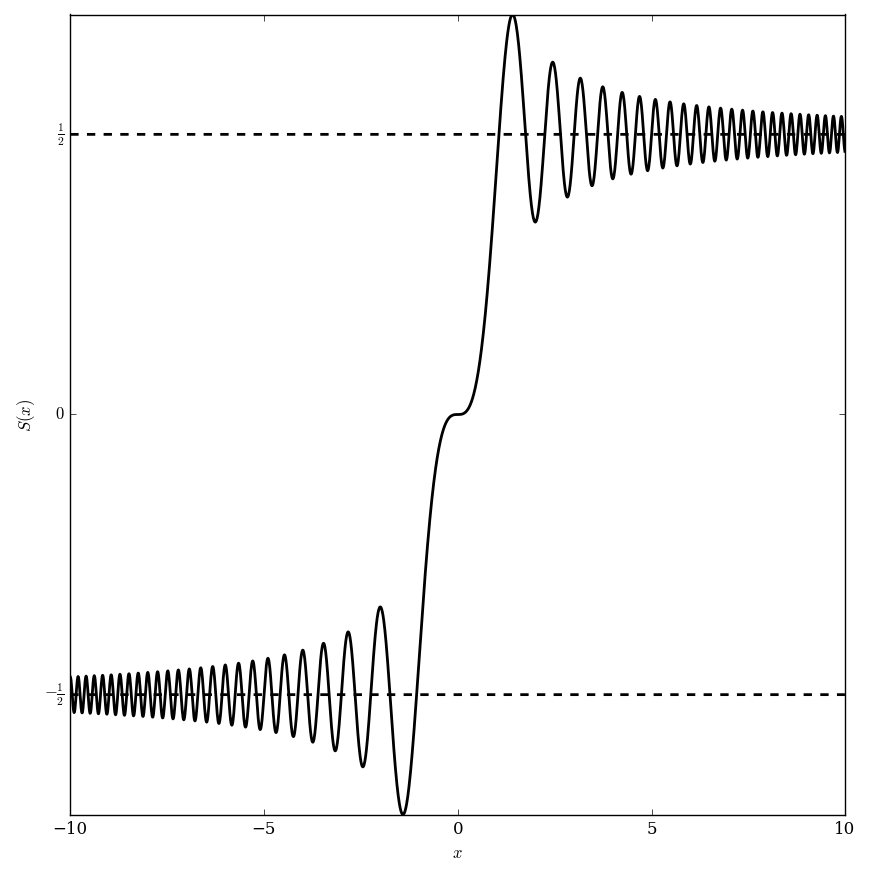
The Fresnel $S$ function is defined by $$S(z)=\int_0^z \sin \left(t^2 \right) \mathrm{d}t.$$ (Note in Abramowitz&Stegun it is defined differently.)
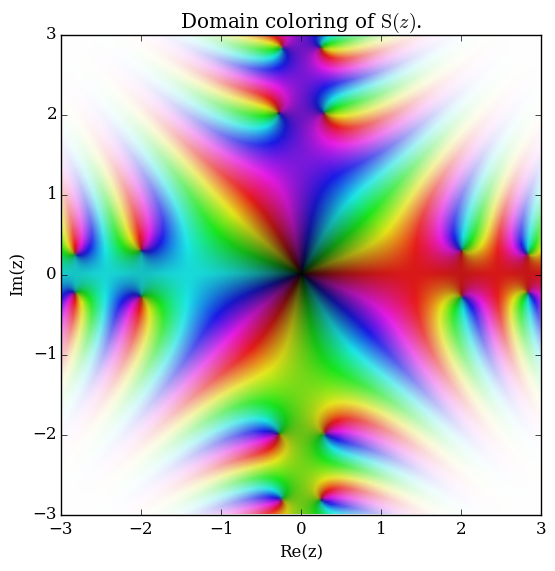
Domain coloring of Fresnel $S$.
Properties
Fresnel S is odd
Taylor series for Fresnel S
Fresnel S in terms of erf
Limiting value of Fresnel S
See Also
Videos
The Fresnel Integral S(x) - How to integrate sin(x^2) (12 February 2015)
Math and Physics: The Fresnel Integrals (12 May 2016)