Difference between revisions of "Reciprocal gamma"
From specialfunctionswiki
(→See Also) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The reciprocal gamma function is | + | The reciprocal gamma function $\dfrac{1}{\Gamma}$ is defined by |
| + | $$\left( \dfrac{1}{\Gamma} \right)(z) =\dfrac{1}{\Gamma(z)},$$ | ||
| + | where $\Gamma$ denotes the [[gamma function]]. | ||
<div align="center"> | <div align="center"> | ||
| Line 11: | Line 13: | ||
=Properties= | =Properties= | ||
| + | [[Reciprocal gamma is entire]]<br /> | ||
[[Reciprocal gamma written as an infinite product]]<br /> | [[Reciprocal gamma written as an infinite product]]<br /> | ||
[[Contour integral representation of reciprocal gamma]]<br /> | [[Contour integral representation of reciprocal gamma]]<br /> | ||
Latest revision as of 10:50, 11 January 2017
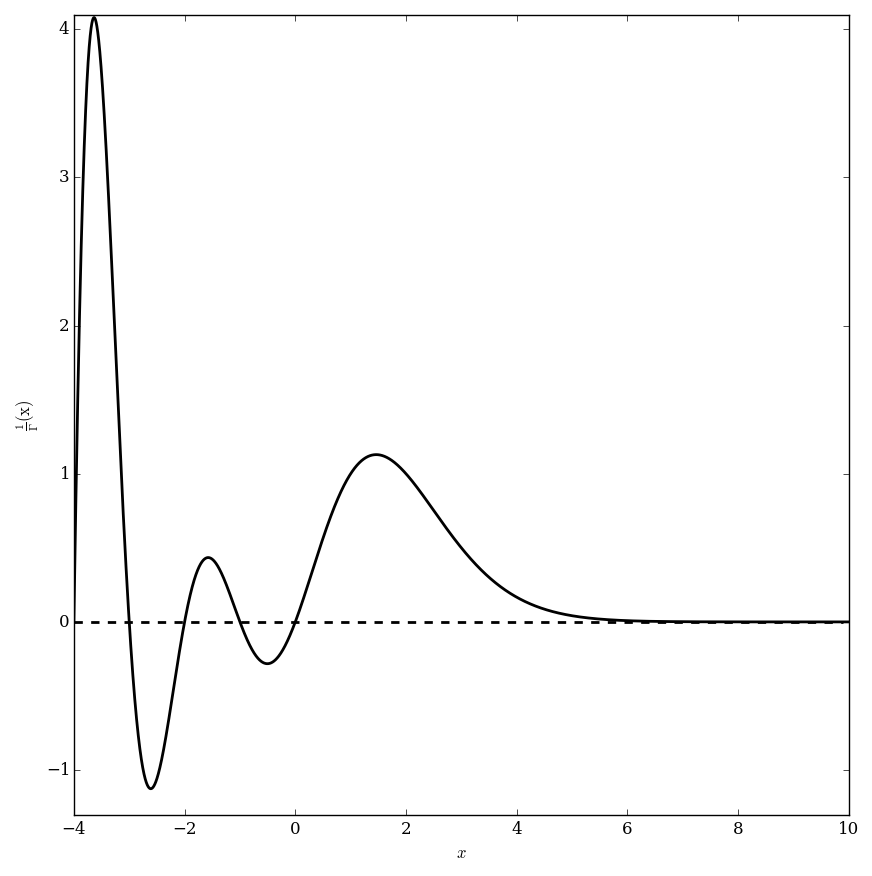
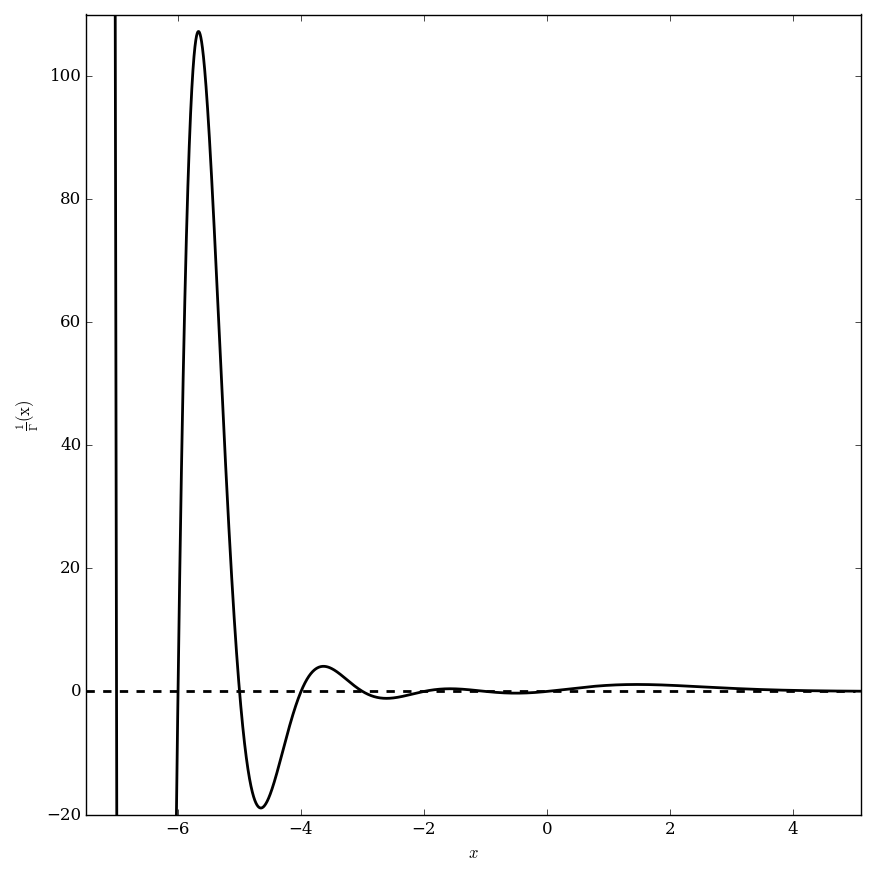
The reciprocal gamma function $\dfrac{1}{\Gamma}$ is defined by $$\left( \dfrac{1}{\Gamma} \right)(z) =\dfrac{1}{\Gamma(z)},$$ where $\Gamma$ denotes the gamma function.
Graph of $\dfrac{1}{\Gamma}$ on $[-4,10]$.
Graph of $\dfrac{1}{\Gamma}$ on $[-7.5,5.1]$.
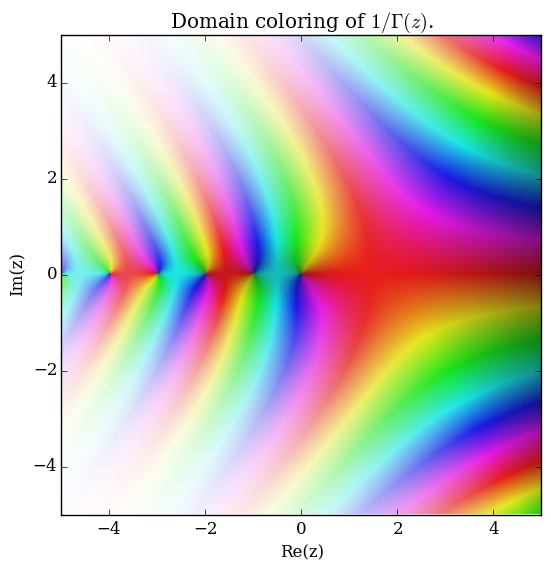
Domain coloring of $\dfrac{1}{\Gamma}$.
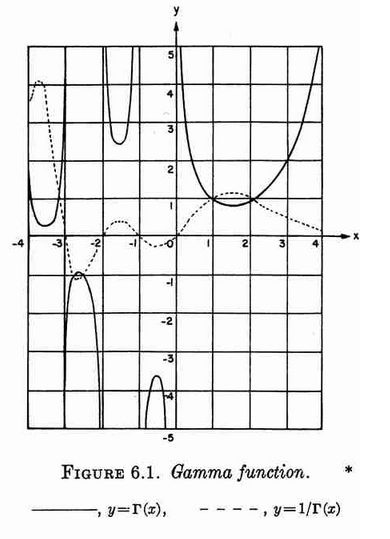
Plot of $\Gamma$ and $\dfrac{1}{\Gamma}$ from Abramowitz&Stegun.
.png)
Properties
Reciprocal gamma is entire
Reciprocal gamma written as an infinite product
Contour integral representation of reciprocal gamma
