Difference between revisions of "Dirichlet beta"
From specialfunctionswiki
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
The Dirichlet $\beta$ function is defined by | The Dirichlet $\beta$ function is defined by | ||
| − | $$\beta( | + | $$\beta(z) = \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k}{(2k+1)^z}.$$ |
Latest revision as of 00:54, 11 December 2016
The Dirichlet $\beta$ function is defined by $$\beta(z) = \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k}{(2k+1)^z}.$$
Graph of $\beta$ on $[-4,4]$.
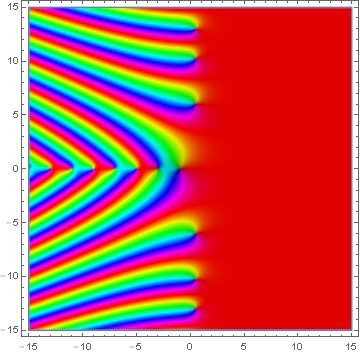
Domain coloring of analytic continuation of $\beta$.
Properties
Catalan's constant using Dirichlet beta
Dirichlet beta in terms of Lerch transcendent
