Difference between revisions of "Cosine integral"
From specialfunctionswiki
(→Videos) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
| − | The cosine integral is defined by | + | The cosine integral, $\mathrm{Ci}$, is defined by |
$$\mathrm{Ci}(z) = -\displaystyle\int_z^{\infty} \dfrac{\cos t}{t} \mathrm{d}t, \quad |\mathrm{arg} z|<\pi.$$ | $$\mathrm{Ci}(z) = -\displaystyle\int_z^{\infty} \dfrac{\cos t}{t} \mathrm{d}t, \quad |\mathrm{arg} z|<\pi.$$ | ||
| Line 19: | Line 19: | ||
=References= | =References= | ||
| − | * | + | * {{BookReference|Special Functions of Mathematical Physics and Chemistry|1956|Ian N. Sneddon|prev=findme|next=Sine integral}}: $\S 5 (5.10)$ |
{{:*-integral functions footer}} | {{:*-integral functions footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 15:43, 11 July 2017
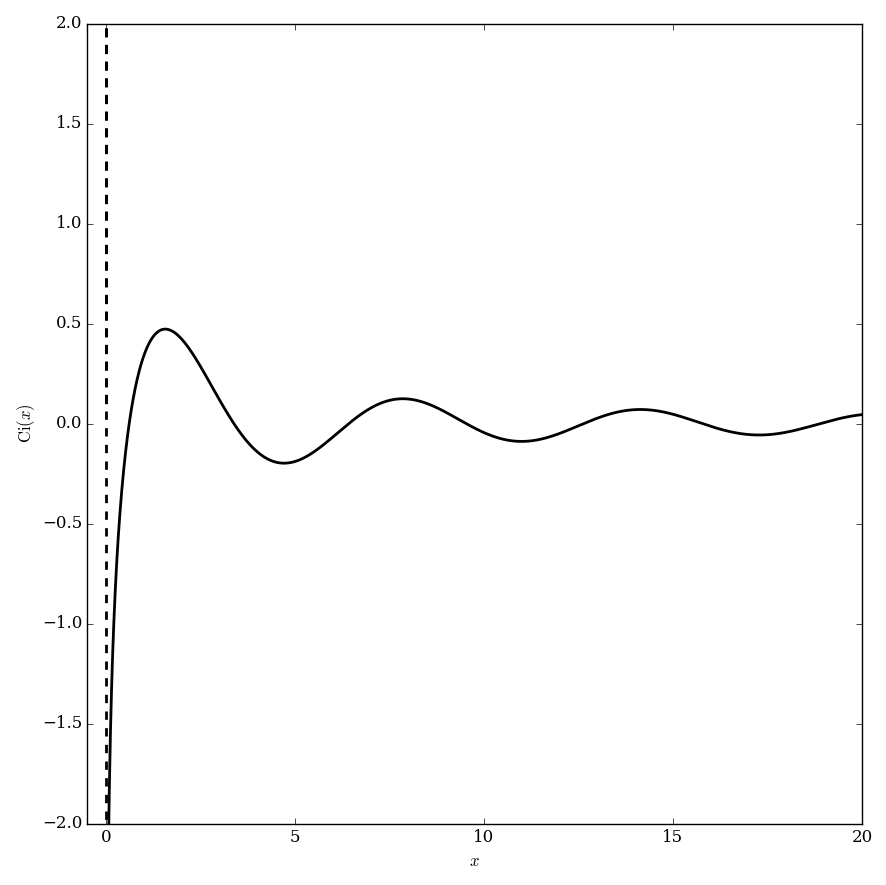
The cosine integral, $\mathrm{Ci}$, is defined by $$\mathrm{Ci}(z) = -\displaystyle\int_z^{\infty} \dfrac{\cos t}{t} \mathrm{d}t, \quad |\mathrm{arg} z|<\pi.$$
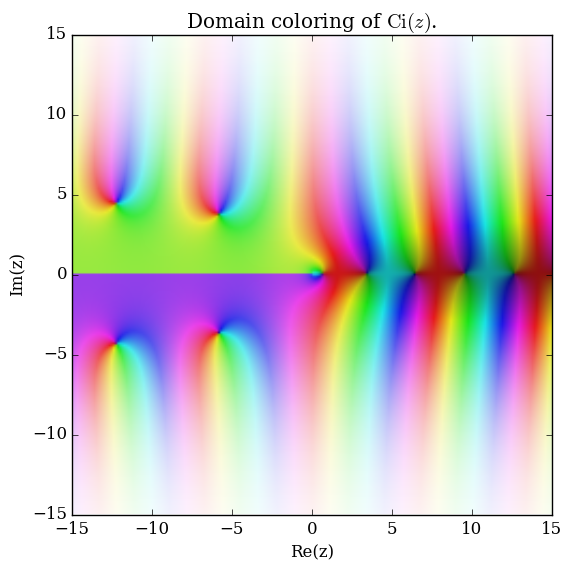
Domain coloring of $\mathrm{Ci}$.
Relationship to other functions
Derivative of cosine integral
Antiderivative of cosine integral
Relationship between exponential integral Ei, cosine integral, and sine integral
Videos
Laplace transform of cosine integral (2 January 2015)
References
- 1956: Ian N. Sneddon: Special Functions of Mathematical Physics and Chemistry ... (previous) ... (next): $\S 5 (5.10)$