Difference between revisions of "Lambert W"
From specialfunctionswiki
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
| − | The Lambert $W$ function is the (multi-valued) | + | The Lambert $W$ function is the (multi-valued) function that satisfies the equation |
| + | $$z=W(z)e^{W(z)}.$$ | ||
<div align="center"> | <div align="center"> | ||
| Line 13: | Line 14: | ||
=Videos= | =Videos= | ||
| − | [https://www.youtube.com/watch?v=AJD8kh3DSAM 6: Recursion, Infinite Tetrations and the Lambert W Function (4 August 2014)] | + | *[https://www.youtube.com/watch?v=AJD8kh3DSAM 6: Recursion, Infinite Tetrations and the Lambert W Function (4 August 2014)] |
| + | |||
| + | =External links= | ||
| + | *[http://arxiv.org/pdf/1003.1628.pdf Having fun with the Lambert $W(x)$ function] | ||
| + | |||
| + | =See also= | ||
| + | [[Lambert W0]]<br /> | ||
| + | [[Lambert W1]]<br /> | ||
=References= | =References= | ||
| − | + | * {{PaperReference|On the Lambert W function|1996|R. M. Corless|author2=G. H. Gonnet|author3=D.E.G. Hare|author4=D.J. Jeffrey|author4=D.E. Knuth|prev=findme|next=findme}} $(1.5)$ | |
| − | |||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 18:24, 16 June 2018
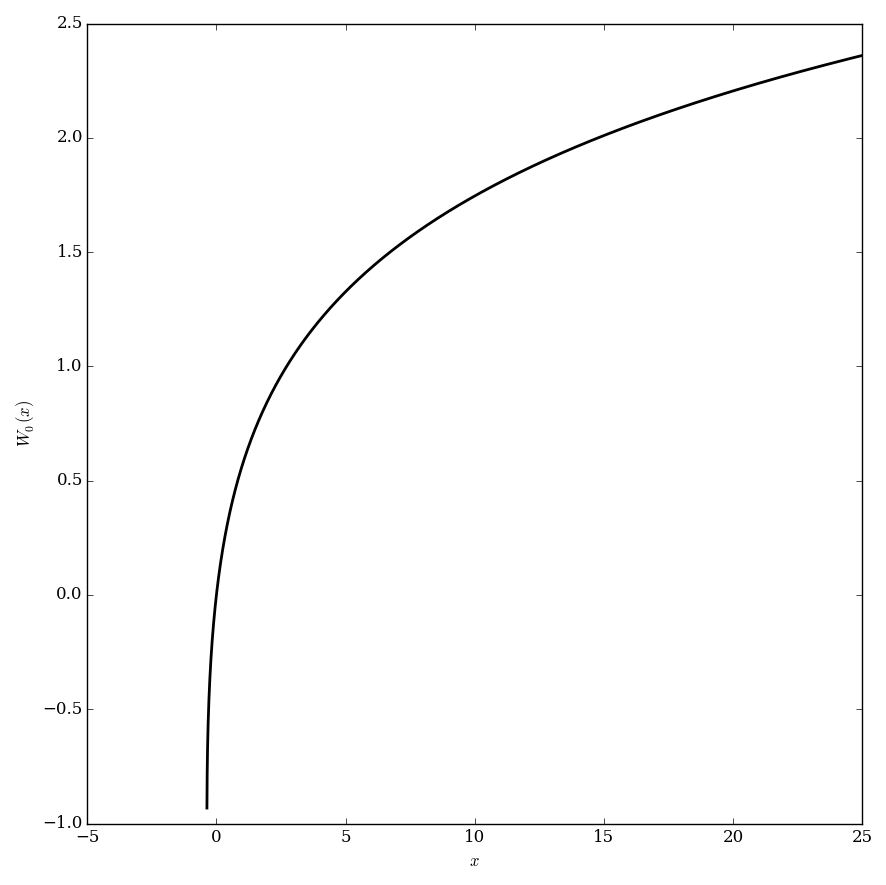
The Lambert $W$ function is the (multi-valued) function that satisfies the equation $$z=W(z)e^{W(z)}.$$
Plot of the principal branch $W_0$.
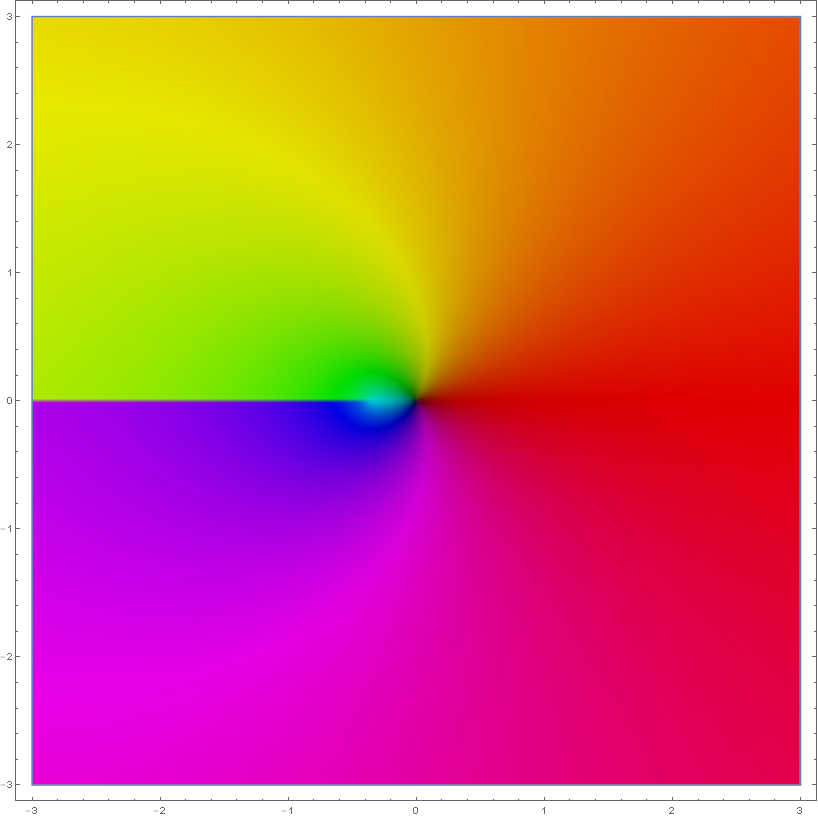
Domain coloring of analytic continuation of branch $W_0(x)$ to $\mathbb{C}$.
Domain coloring of analytic continuation of branch $W_{-1}(x)$ to $\mathbb{C}$.
Properties
Videos
External links
See also
References
- R. M. Corless, G. H. Gonnet, D.E.G. Hare and D.E. Knuth: On the Lambert W function (1996)... (previous)... (next) $(1.5)$
