Difference between revisions of "Polylogarithm"
From specialfunctionswiki
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
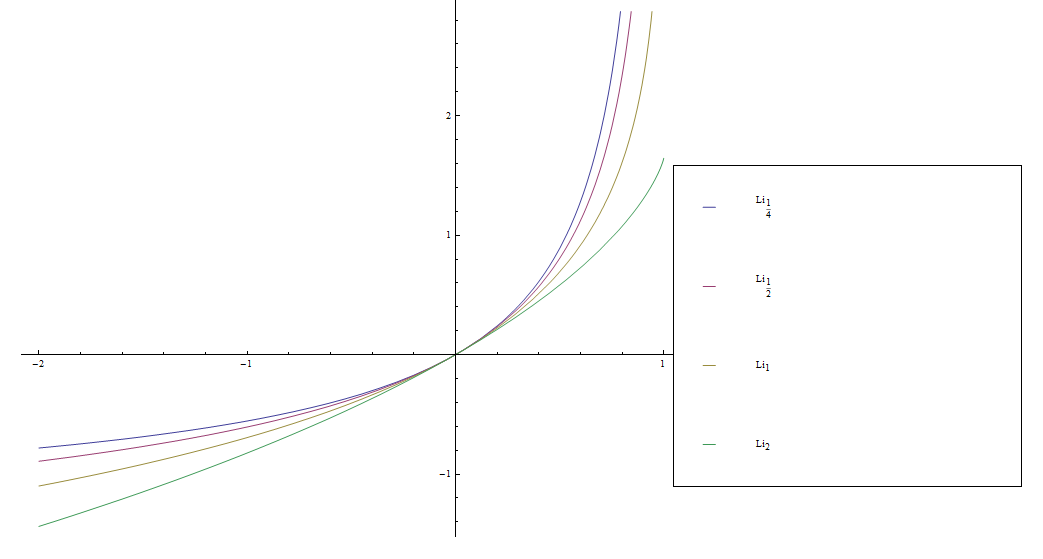
The polylogarithm $\mathrm{Li}_s$ is defined by the formula for $|z|<1$ by | The polylogarithm $\mathrm{Li}_s$ is defined by the formula for $|z|<1$ by | ||
| − | $$\mathrm{Li}_s(z) = \sum_{k=1}^{\infty} \dfrac{z^k}{k^ | + | $$\mathrm{Li}_s(z) = \sum_{k=1}^{\infty} \dfrac{z^k}{k^s} = z + \dfrac{z^2}{2^s} + \dfrac{z^3}{3^s} + \ldots$$ |
A special case of the polylogarithm with $s=2$ is called a [[dilogarithm]]. | A special case of the polylogarithm with $s=2$ is called a [[dilogarithm]]. | ||
| Line 18: | Line 18: | ||
=References= | =References= | ||
| + | |||
| + | {{:Logarithm and friends footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 20:28, 25 June 2017
The polylogarithm $\mathrm{Li}_s$ is defined by the formula for $|z|<1$ by $$\mathrm{Li}_s(z) = \sum_{k=1}^{\infty} \dfrac{z^k}{k^s} = z + \dfrac{z^2}{2^s} + \dfrac{z^3}{3^s} + \ldots$$ A special case of the polylogarithm with $s=2$ is called a dilogarithm.
Various polylogarithms plotted on $[-2,1]$.
Properties
Lerch transcendent polylogarithm
Legendre chi in terms of polylogarithm
