Difference between revisions of "Beta"
From specialfunctionswiki
| Line 1: | Line 1: | ||
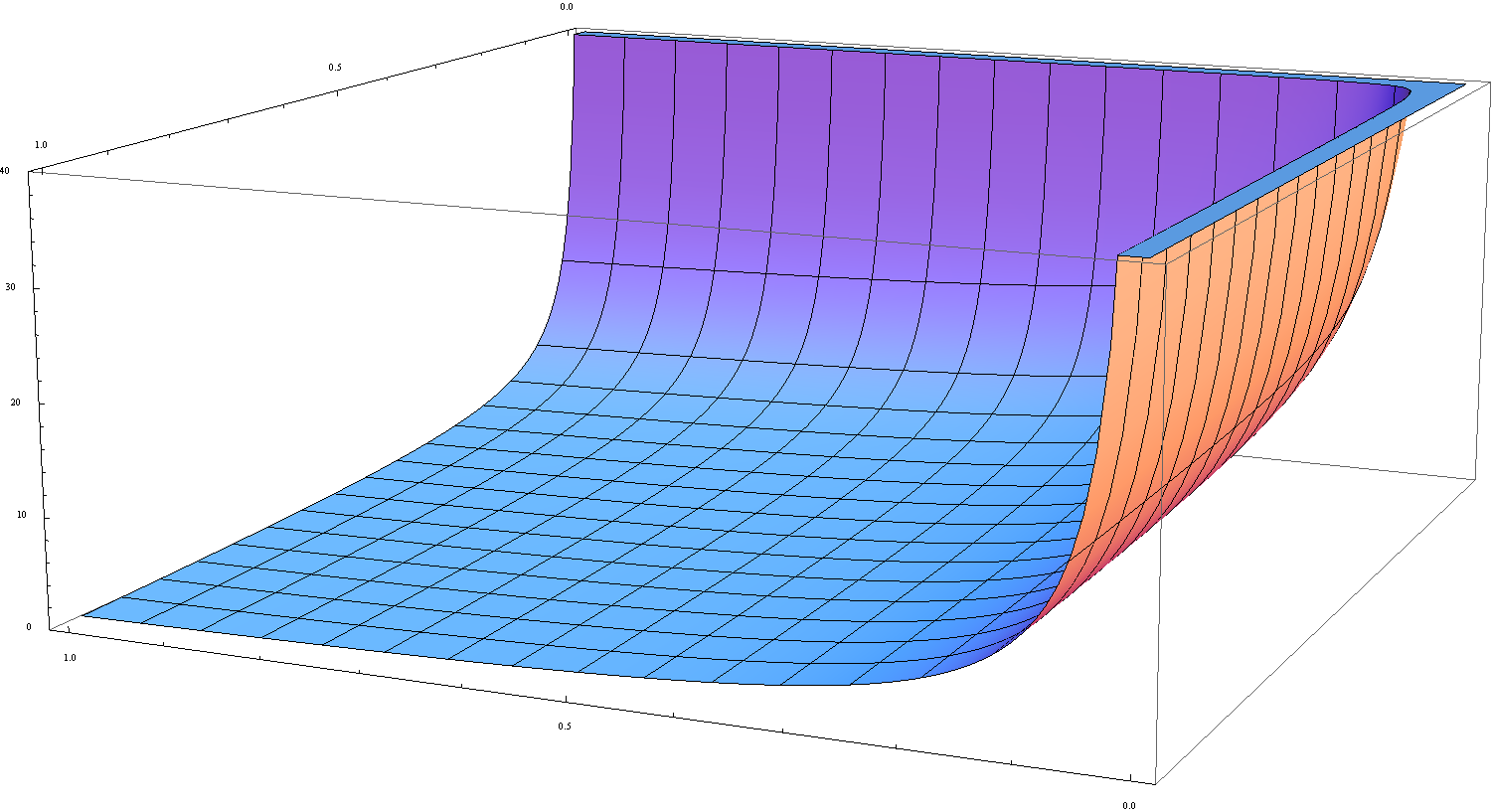
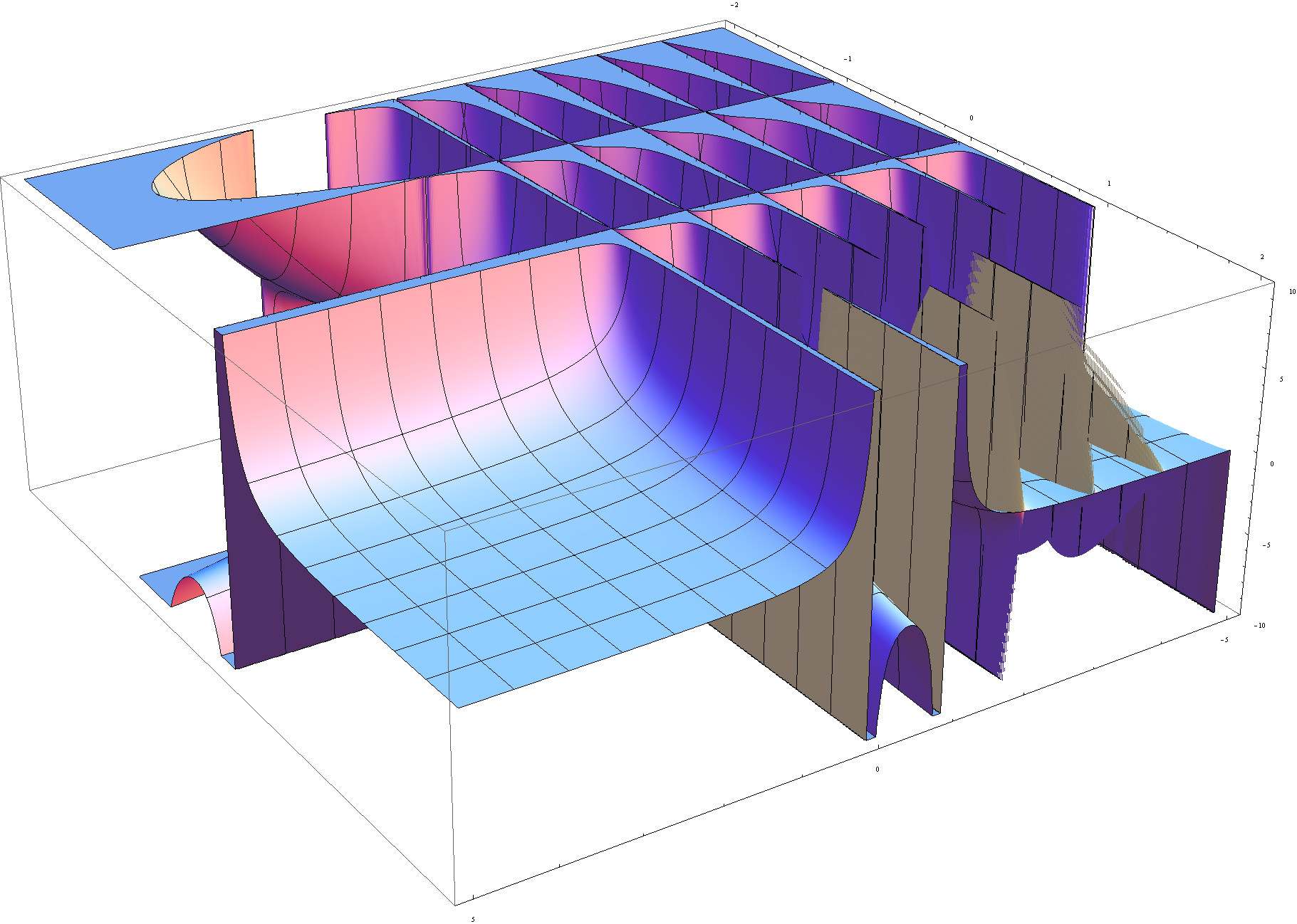
The $\beta$ function is defined by the formula | The $\beta$ function is defined by the formula | ||
$$B(x,y)=\displaystyle\int_0^1 t^{x-1}(1-t)^{y-1}dt.$$ | $$B(x,y)=\displaystyle\int_0^1 t^{x-1}(1-t)^{y-1}dt.$$ | ||
| − | |||
| − | + | <div align="center"> | |
| + | <gallery> | ||
| + | File:Beta2.png | ||
| + | File:Beta.png | ||
| + | </gallery> | ||
| + | </div> | ||
| + | [[500px]] | ||
| + | |||
| + | [[500px]] | ||
=Properties= | =Properties= | ||
Revision as of 05:26, 16 January 2015
The $\beta$ function is defined by the formula $$B(x,y)=\displaystyle\int_0^1 t^{x-1}(1-t)^{y-1}dt.$$
Properties
Theorem: The following formula holds: $$B(x,y)=\dfrac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)},$$ where $\Gamma$ denotes the gamma function.
Proof: █
Theorem: $B(x,y)=B(y,x)$
Proof: █
Theorem: (i) $B(x+1,y)=\dfrac{x}{x+y} B(x,y)$
(ii) $B(x,y+1)=\dfrac{y}{x+y}B(x,y)$
Proof: █
References
Bell. Special Functions