Difference between revisions of "Arccos"
From specialfunctionswiki
(Created page with "The $\mathrm{arccos}$ function is the inverse function of the cosine function. 500px") |
|||
| Line 2: | Line 2: | ||
[[File:Arccos.png|500px]] | [[File:Arccos.png|500px]] | ||
| + | |||
| + | =Properties= | ||
| + | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
| + | <strong>Proposition:</strong> | ||
| + | $$\dfrac{d}{dz} \mathrm{arccos}(z) = -\dfrac{1}{\sqrt{1-z^2}}$$ | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <strong>Proof:</strong> █ | ||
| + | </div> | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
| + | <strong>Proposition:</strong> | ||
| + | $$\int \mathrm{arccos}(z) dz = z\mathrm{arccos}(z)-\sqrt{1-z^2}+C$$ | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <strong>Proof:</strong> █ | ||
| + | </div> | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
| + | <strong>Proposition:</strong> | ||
| + | $$\mathrm{arccos}(z)=\mathrm{arcsec} \left( \dfrac{1}{z} \right)$$ | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <strong>Proof:</strong> █ | ||
| + | </div> | ||
| + | </div> | ||
| + | </div> | ||
Revision as of 01:29, 19 October 2014
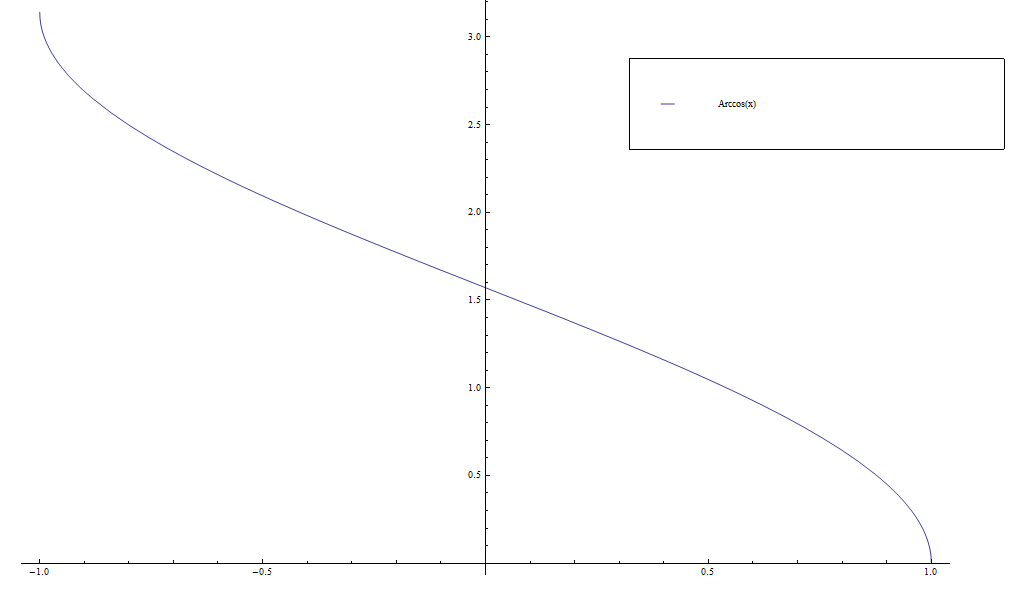
The $\mathrm{arccos}$ function is the inverse function of the cosine function.
Properties
Proposition: $$\dfrac{d}{dz} \mathrm{arccos}(z) = -\dfrac{1}{\sqrt{1-z^2}}$$
Proof: █
</div>
Proposition: $$\int \mathrm{arccos}(z) dz = z\mathrm{arccos}(z)-\sqrt{1-z^2}+C$$
Proof: █
</div>
Proposition: $$\mathrm{arccos}(z)=\mathrm{arcsec} \left( \dfrac{1}{z} \right)$$
Proof: █
</div>