Difference between revisions of "Lambert W"
From specialfunctionswiki
| Line 4: | Line 4: | ||
<gallery> | <gallery> | ||
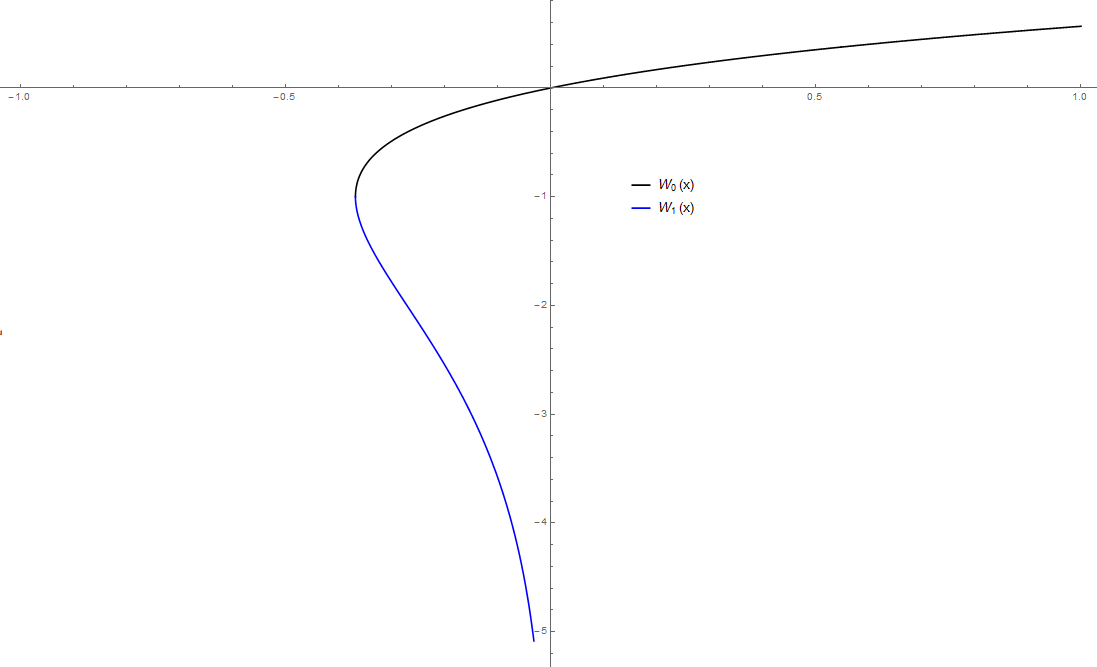
File:lambertwplot.png|Graph of branches $W_0(x)$ and $W_1(x)$ on $[-1,1]$. | File:lambertwplot.png|Graph of branches $W_0(x)$ and $W_1(x)$ on $[-1,1]$. | ||
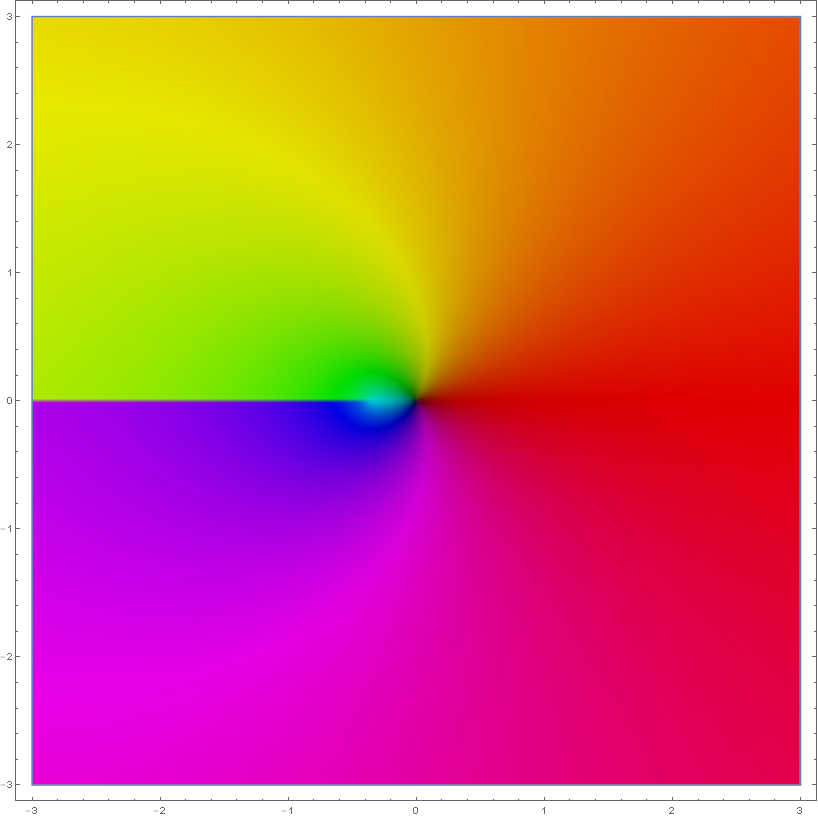
| + | File:Complexlambertw0.png|[[Domain coloring]] of [[analytic continuation]] of branch $W_0(x)$ to $\mathbb{C}$. | ||
| + | File:Complexlambertw-1.png|[[Domain coloring]] of [[analytic continuation]] of branch $W_{-1}(x)$ to $\mathbb{C}$. | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
Revision as of 20:35, 19 February 2015
The Lambert $W$ function is the (multi-valued) inverse of the function $g(x)=xe^{x}$. The function $g$ is not injective because its graph does not pass the "horizontal line test". Therefore the inverse function is multi-valued and not unique. This yields two branches of the $W$ function.
Graph of branches $W_0(x)$ and $W_1(x)$ on $[-1,1]$.
Domain coloring of analytic continuation of branch $W_0(x)$ to $\mathbb{C}$.
Domain coloring of analytic continuation of branch $W_{-1}(x)$ to $\mathbb{C}$.
