Difference between revisions of "Riemann xi"
From specialfunctionswiki
| Line 1: | Line 1: | ||
| − | The Riemann $\xi$ function is defined by the formula | + | The Riemann $\xi$ function (sometimes called the Riemann $\Xi$ function) is defined by the formula |
$$\xi(z)=\dfrac{z}{2}(z-1)\pi^{-\frac{z}{2}}\Gamma\left(\dfrac{z}{2}\right)\zeta(z),$$ | $$\xi(z)=\dfrac{z}{2}(z-1)\pi^{-\frac{z}{2}}\Gamma\left(\dfrac{z}{2}\right)\zeta(z),$$ | ||
where $\Gamma$ denotes the [[gamma function]] and $\zeta$ denotes the [[Riemann zeta function]]. | where $\Gamma$ denotes the [[gamma function]] and $\zeta$ denotes the [[Riemann zeta function]]. | ||
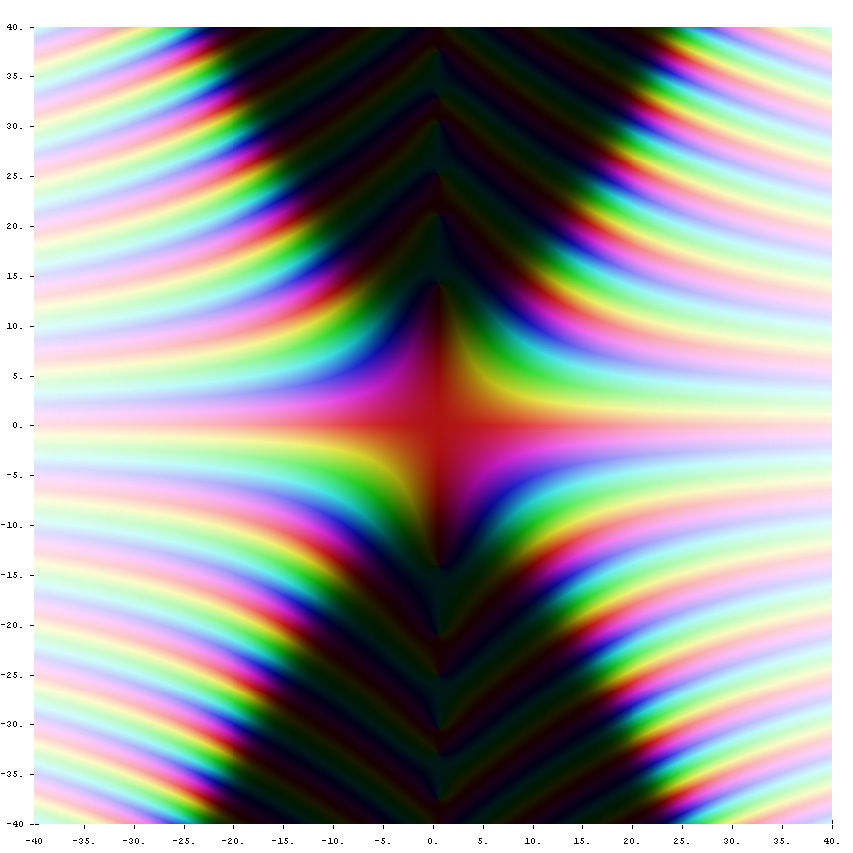
[[File:Complex Riemann Xi.jpg|500px]] | [[File:Complex Riemann Xi.jpg|500px]] | ||
Revision as of 17:34, 19 February 2015
The Riemann $\xi$ function (sometimes called the Riemann $\Xi$ function) is defined by the formula $$\xi(z)=\dfrac{z}{2}(z-1)\pi^{-\frac{z}{2}}\Gamma\left(\dfrac{z}{2}\right)\zeta(z),$$ where $\Gamma$ denotes the gamma function and $\zeta$ denotes the Riemann zeta function.