Difference between revisions of "Lambert W"
From specialfunctionswiki
| Line 11: | Line 11: | ||
=References= | =References= | ||
[http://arxiv.org/pdf/1003.1628.pdf Having fun with the Lambert $W(x)$ function] | [http://arxiv.org/pdf/1003.1628.pdf Having fun with the Lambert $W(x)$ function] | ||
| + | |||
| + | =Videos= | ||
| + | [https://www.youtube.com/watch?v=AJD8kh3DSAM 6: Recursion, Infinite Tetrations and the Lambert W Function] | ||
Revision as of 02:28, 4 June 2015
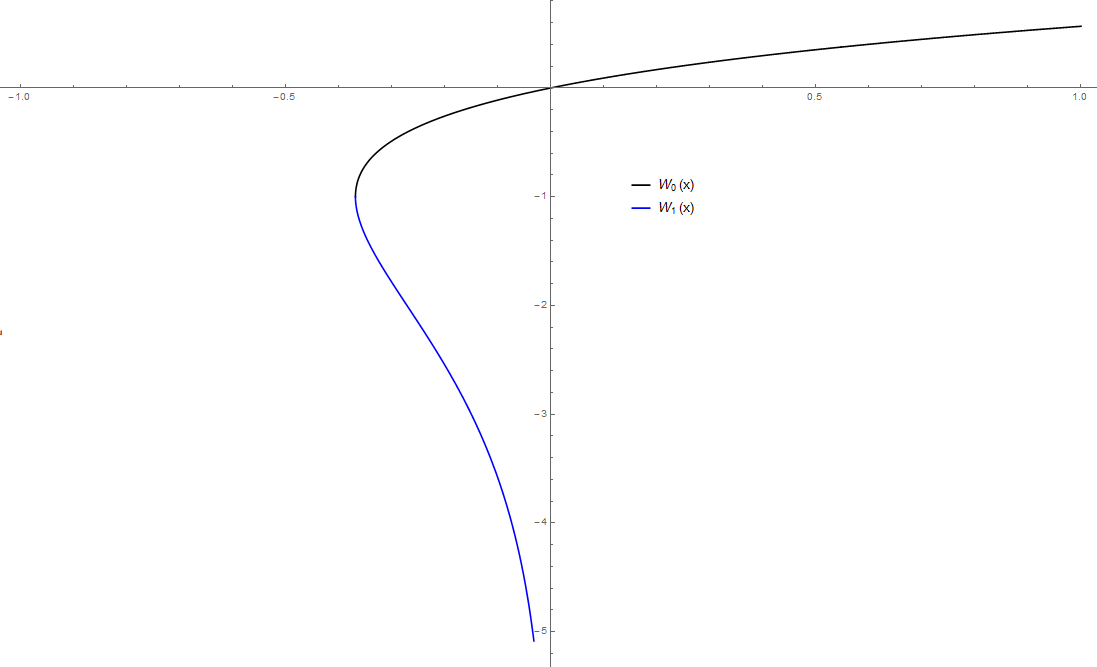
The Lambert $W$ function is the (multi-valued) inverse of the function $g(x)=xe^{x}$. The function $g$ is not injective because its graph does not pass the "horizontal line test". Therefore the inverse function is multi-valued and not unique. This yields two branches of the $W$ function.
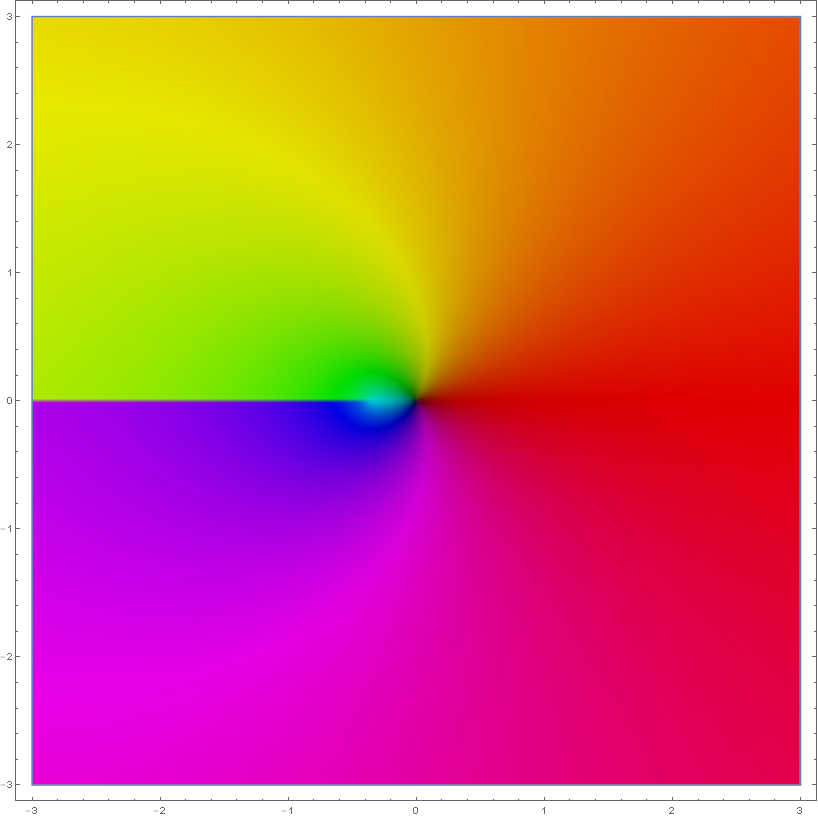
Domain coloring of analytic continuation of branch $W_0(x)$ to $\mathbb{C}$.
Domain coloring of analytic continuation of branch $W_{-1}(x)$ to $\mathbb{C}$.
References
Having fun with the Lambert $W(x)$ function
Videos
6: Recursion, Infinite Tetrations and the Lambert W Function