Difference between revisions of "Arccos"
| Line 39: | Line 39: | ||
=References= | =References= | ||
[http://mathworld.wolfram.com/InverseCosine.html Weisstein, Eric W. "Inverse Cosine." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/InverseCosine.html] | [http://mathworld.wolfram.com/InverseCosine.html Weisstein, Eric W. "Inverse Cosine." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/InverseCosine.html] | ||
| + | |||
| + | =See Also= | ||
| + | [[Cosine]] <br /> | ||
| + | [[Cosh]] <br /> | ||
| + | [[Arccosh]] | ||
<center>{{:Inverse trigonometric functions footer}}</center> | <center>{{:Inverse trigonometric functions footer}}</center> | ||
Revision as of 18:36, 11 November 2015
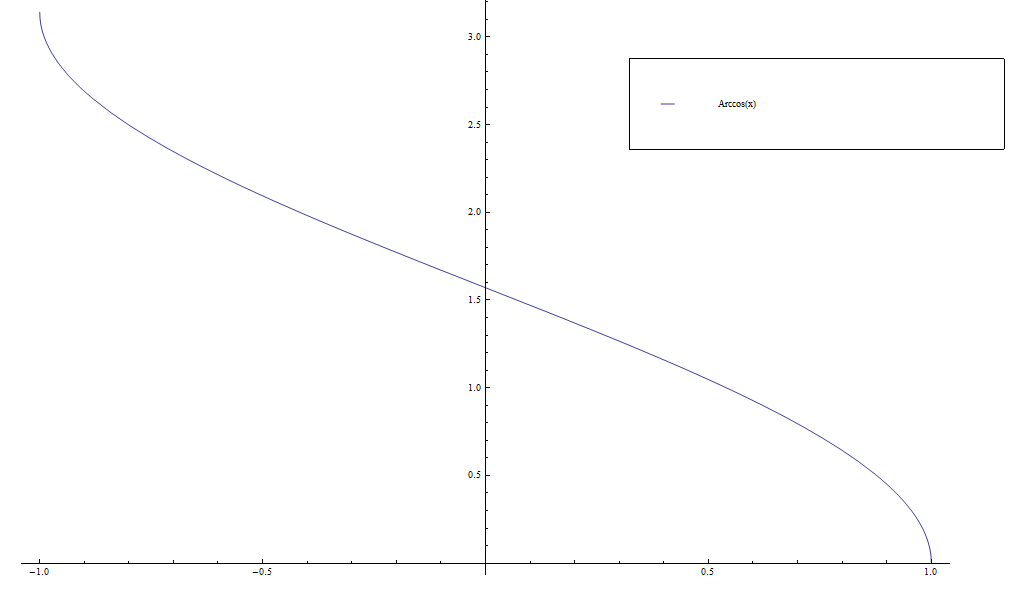
The function $\mathrm{arccos} \colon [-1,1] \longrightarrow [0,\pi]$ is the inverse function of the cosine function.
Graph of $\mathrm{arccos}$ on $[-1,1]$.
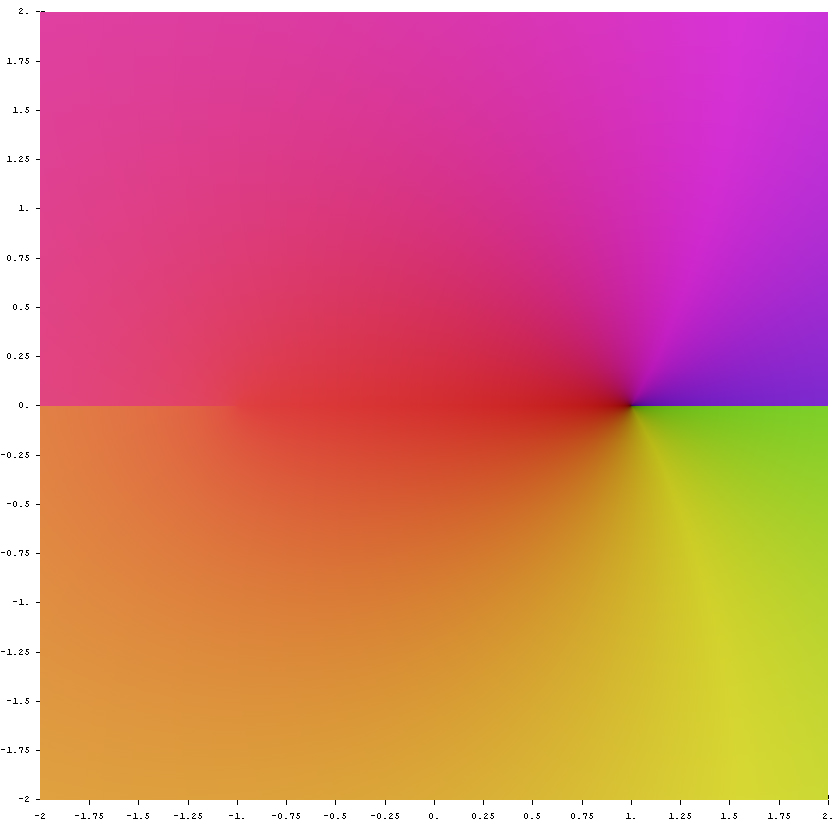
Domain coloring of analytic continuation of $\mathrm{arccos}$.
Properties
Proposition: $\dfrac{d}{dz} \mathrm{arccos}(z) = -\dfrac{1}{\sqrt{1-z^2}}$
Proof: If $\theta=\mathrm{arccos}(z)$ then $\cos(\theta)=z$. Now use implicit differentiation with respect to $z$ to get
$$-\sin(\theta)\theta'=1.$$
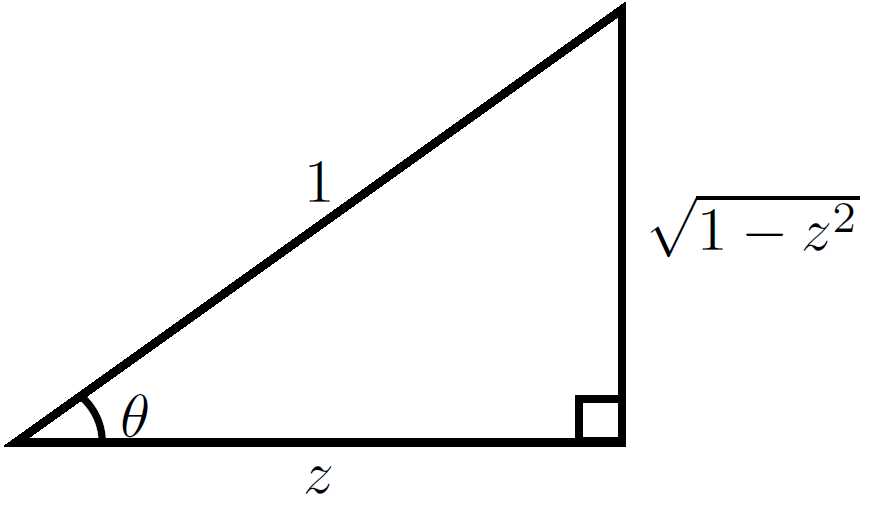
The following image shows that $\sin(\mathrm{arccos}(z))=\sqrt{1-z^2}$:
).png)
Hence substituting back in $\theta=\mathrm{arccos}(z)$ yields the formula
$$\dfrac{d}{dz} \mathrm{arccos}(z) = -\dfrac{1}{\sin(\mathrm{arccos}(z))} = -\dfrac{1}{\sqrt{1-z^2}}.█$$
Proposition: $\displaystyle\int \mathrm{arccos}(z) dz = z\mathrm{arccos}(z)-\sqrt{1-z^2}+C$
Proof: █
Proposition: $\mathrm{arccos}(z)=\mathrm{arcsec} \left( \dfrac{1}{z} \right)$
Proof: █
