Difference between revisions of "Thomae function"
From specialfunctionswiki
(→Properties) |
|||
| Line 1: | Line 1: | ||
| − | Thomae's function is given by the formula | + | Thomae's function (sometimes called the popcorn function) is given by the formula |
$$f(x) =\begin{cases} | $$f(x) =\begin{cases} | ||
1 & \text{if } x= 0 \\ | 1 & \text{if } x= 0 \\ | ||
| Line 29: | Line 29: | ||
<div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
| − | <strong>Theorem:</strong> The [[Thomae function]] $f(x)$ is | + | <strong>Theorem:</strong> The [[Thomae function]] $f(x)$ is [[Riemann integral|Riemann integrable]] and |
$$\displaystyle\int_0^1 f(x) dx = 0.$$ | $$\displaystyle\int_0^1 f(x) dx = 0.$$ | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| Line 35: | Line 35: | ||
</div> | </div> | ||
</div> | </div> | ||
| + | |||
| + | =Videos= | ||
| + | [https://www.youtube.com/watch?v=HeIU5lLtHyQ Thomae Function by Douglas Harder]<br /> | ||
| + | [https://www.youtube.com/watch?v=Xu5Y6DqzN7Q Thomae Function by Bret Benesh] | ||
| + | |||
| + | =See also= | ||
| + | [https://kbeanland.files.wordpress.com/2010/01/beanlandrobstevensonmonthly.pdf Modifications of Thomae's Function and Differentiability] | ||
| + | |||
| + | =References= | ||
| + | [https://www.math.washington.edu/~morrow/334_10/thomae.pdf] | ||
| + | [https://math.la.asu.edu/~kuiper/371files/ThomaeFunction.pdf] | ||
| + | [http://math.stackexchange.com/questions/530097/proof-of-continuity-of-thomae-function-at-irrationals] | ||
Revision as of 20:58, 11 April 2015
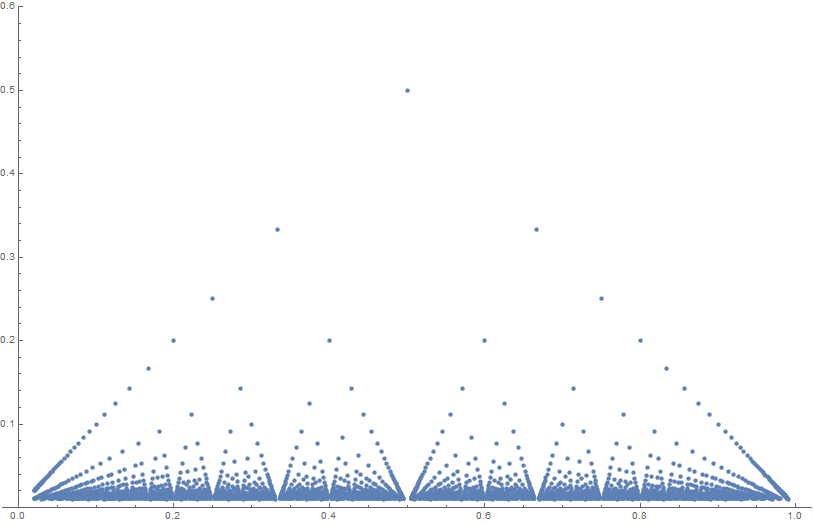
Thomae's function (sometimes called the popcorn function) is given by the formula $$f(x) =\begin{cases} 1 & \text{if } x= 0 \\ \tfrac1{q} & \text{if } x = \tfrac{p}{q}\\ 0 & \text{if } x \in \mathbb{R}-\mathbb{Q}. \end{cases}$$
Contents
Properties
Theorem: The Thomae function is continuous at all irrational numbers and discontinuous at all rational numbers.
Proof: █
Theorem: The Thomae function has a (strict) local maximum at each rational number.
Proof: █
Theorem: The Thomae function $f(x)$ is Riemann integrable and $$\displaystyle\int_0^1 f(x) dx = 0.$$
Proof: █
Videos
Thomae Function by Douglas Harder
Thomae Function by Bret Benesh
See also
Modifications of Thomae's Function and Differentiability