Difference between revisions of "Thomae function"
From specialfunctionswiki
(→References) |
|||
| Line 47: | Line 47: | ||
[https://math.la.asu.edu/~kuiper/371files/ThomaeFunction.pdf]<br /> | [https://math.la.asu.edu/~kuiper/371files/ThomaeFunction.pdf]<br /> | ||
[http://math.stackexchange.com/questions/530097/proof-of-continuity-of-thomae-function-at-irrationals]<br /> | [http://math.stackexchange.com/questions/530097/proof-of-continuity-of-thomae-function-at-irrationals]<br /> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Revision as of 18:29, 24 May 2016
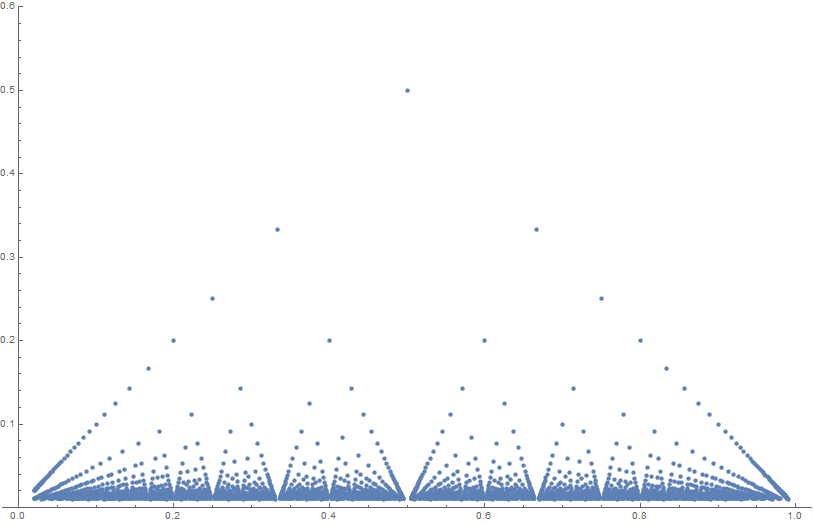
Thomae's function (sometimes called the popcorn function, raindrop function, Stars over Babylon) is given by the formula $$f(x) =\begin{cases} 1 & \text{if } x= 0 \\ \tfrac1{q} & \text{if } x = \tfrac{p}{q}\\ 0 & \text{if } x \in \mathbb{R}-\mathbb{Q}. \end{cases}$$
Plot of the Thomae function.
Contents
Properties
Theorem: The Thomae function is continuous at all irrational numbers and discontinuous at all rational numbers.
Proof: █
Theorem: The Thomae function has a (strict) local maximum at each rational number.
Proof: █
Theorem: The Thomae function $f(x)$ is Riemann integrable and $$\displaystyle\int_0^1 f(x) dx = 0.$$
Proof: █
Videos
Thomae Function by Douglas Harder
Thomae Function by Bret Benesh
See also
Modifications of Thomae's Function and Differentiability
