Difference between revisions of "Hankel H (1)"
From specialfunctionswiki
| Line 5: | Line 5: | ||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
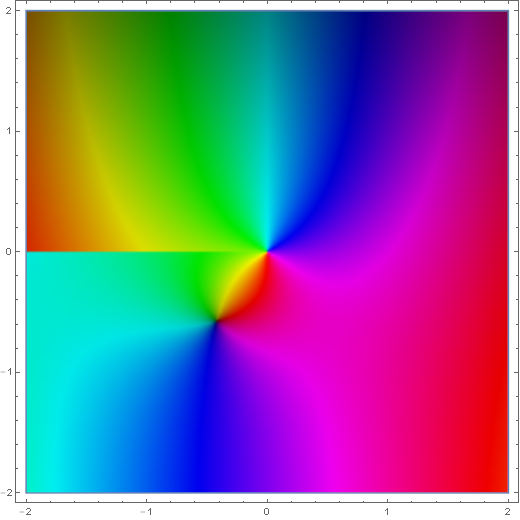
| − | File:Complex hankel H1 sub 1.png|[[Domain coloring]] of [[analytic continuation]]. | + | File:Complex hankel H1 sub 1.png|[[Domain coloring]] of [[analytic continuation]] of $H_1}^{(1)}(z)$. |
</gallery> | </gallery> | ||
</div> | </div> | ||
Revision as of 19:57, 19 May 2015
The Hankel functions of the first kind are defined by $$H_{\nu}^{(1)}(z)=J_{\nu}(z)+iY_{\nu}(z),$$ where $J_{\nu}$ is the Bessel function of the first kind and $Y_{\nu}$ is the Bessel function of the second kind. Note the similarity of these functions to the Hankel functions of the second kind.
Domain coloring of analytic continuation of $H_1}^{(1)}(z)$.