Difference between revisions of "Tanhc"
From specialfunctionswiki
| Line 19: | Line 19: | ||
<center>{{:*-c functions footer}}</center> | <center>{{:*-c functions footer}}</center> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Revision as of 18:46, 24 May 2016
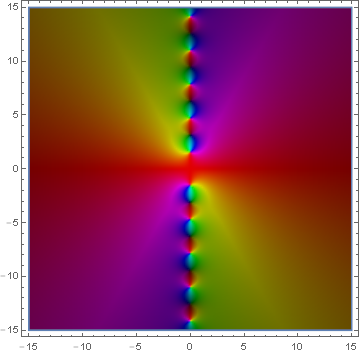
The $\mathrm{tanhc}$ function is defined by $$\mathrm{tanhc}(z) = \dfrac{\mathrm{tanh}(z)}{z}.$$
Domain coloring of analytic continuation of $\mathrm{tanhc}(z)$.
Properties
Theorem: The following formula holds: $$\dfrac{d}{dz} \mathrm{tanhc}(z) = \dfrac{\mathrm{sech}^2(z)}{z}-\dfrac{\mathrm{tanh(z)}}{z^2}.$$
Proof: █