Difference between revisions of "Fresnel S"
From specialfunctionswiki
| Line 5: | Line 5: | ||
<gallery> | <gallery> | ||
File:Fresnel.png| Fresnel integrals on $\mathbb{R}$. | File:Fresnel.png| Fresnel integrals on $\mathbb{R}$. | ||
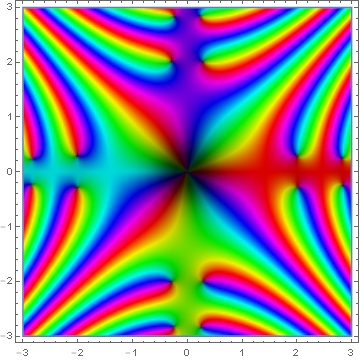
| + | File:Domain coloring fresnel s.png | [[Domain coloring]] of [[analytic continuation]] of Fresnel $S$. | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
Revision as of 18:54, 25 July 2015
The Fresnel $S$ function is defined by $$S(x)=\int_0^x \sin(t^2) dt.$$
- Fresnel.png
Fresnel integrals on $\mathbb{R}$.
Domain coloring of analytic continuation of Fresnel $S$.
Properties
Theorem: The following limit is known: $$\displaystyle\lim_{x \rightarrow \infty} S(x) = \displaystyle\int_0^{\infty} \sin(t^2)dt = \sqrt{ \dfrac{\pi}{8}}.$$
Proof: █
Videos
The Fresnel Integral S(x) - How to integrate sin(x^2)