Difference between revisions of "Lower incomplete gamma"
From specialfunctionswiki
| Line 9: | Line 9: | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Latest revision as of 18:32, 24 May 2016
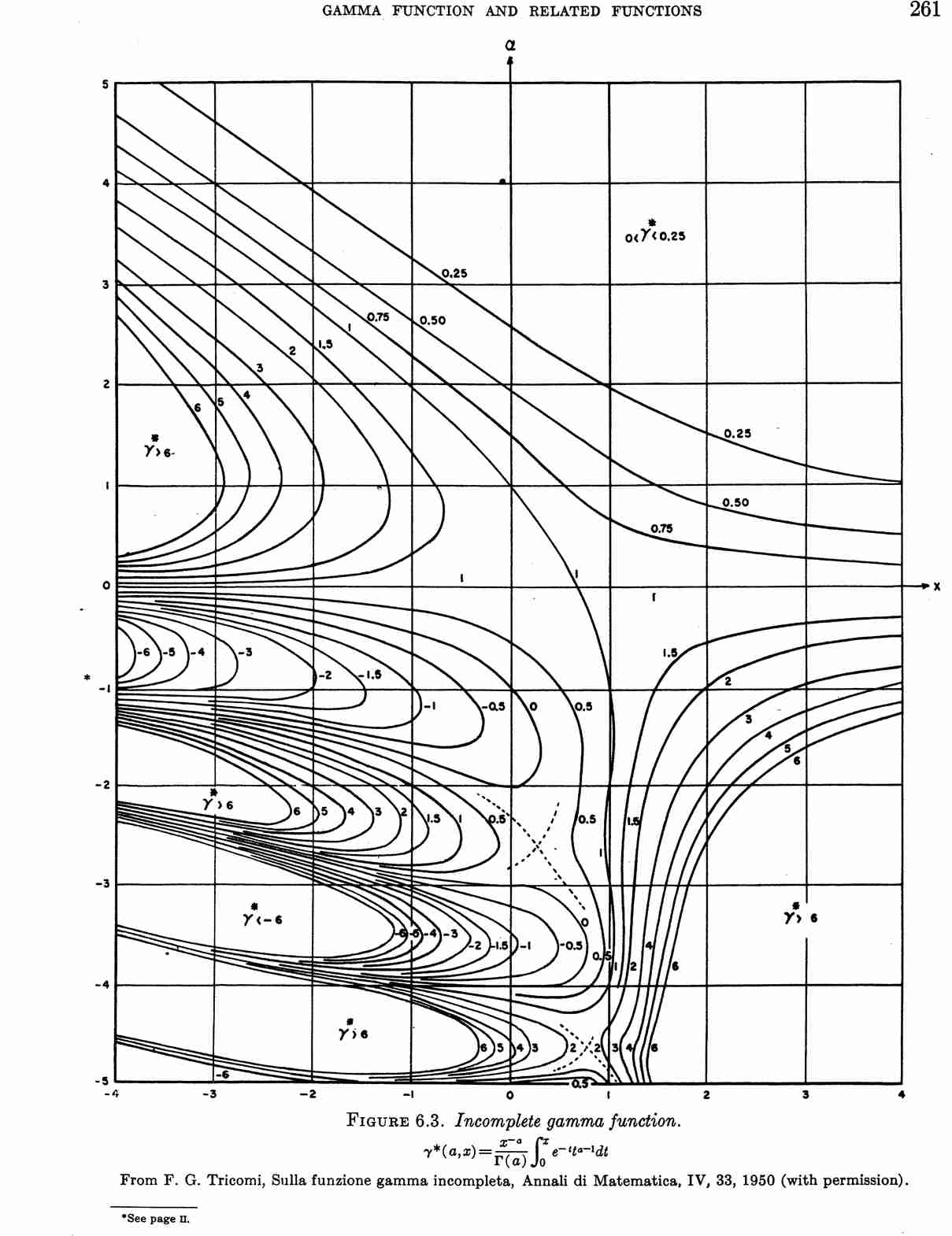
The lower incomplete gamma function is defined for $\mathrm{Re}(a)>0$ by $$\gamma(a,x)=\displaystyle\int_0^x e^{-t}t^{a-1}dt.$$ A single-valued analytic function of $a$ and $x$ can be defined as $$\gamma^*(a,x)=\dfrac{x^{-a}}{\Gamma(a)} \gamma(a,x).$$
The $\gamma^*$ function from Abramowitz&Stegun.
.jpg)
