Difference between revisions of "Fresnel C"
From specialfunctionswiki
| Line 17: | Line 17: | ||
</div> | </div> | ||
</div> | </div> | ||
| + | |||
| + | =See Also= | ||
| + | [[Fresnel S]] | ||
=Videos= | =Videos= | ||
Revision as of 10:29, 30 December 2015
The Fresnel C function is defined by the formula $$C(x)=\int_0^x \cos(t^2) dt.$$
- Fresnel.png
Fresnel integrals on $\mathbb{R}$.
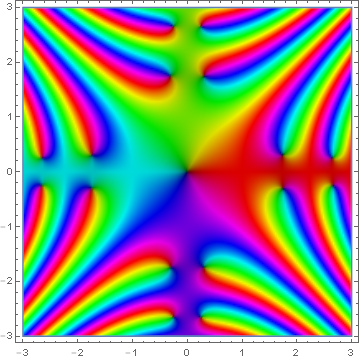
Domain coloring of analytic continuation of Fresnel $C$.
Properties
Theorem: The following limit is known: $$\displaystyle\lim_{x \rightarrow \infty} C(x) = \displaystyle\int_0^{\infty} \cos(t^2)dt = \sqrt{ \dfrac{\pi}{8}}.$$
Proof: █
See Also
Videos
How to integrate cos(x^2) - The Fresnel Integral C(x)