Difference between revisions of "Anger function"
| Line 4: | Line 4: | ||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
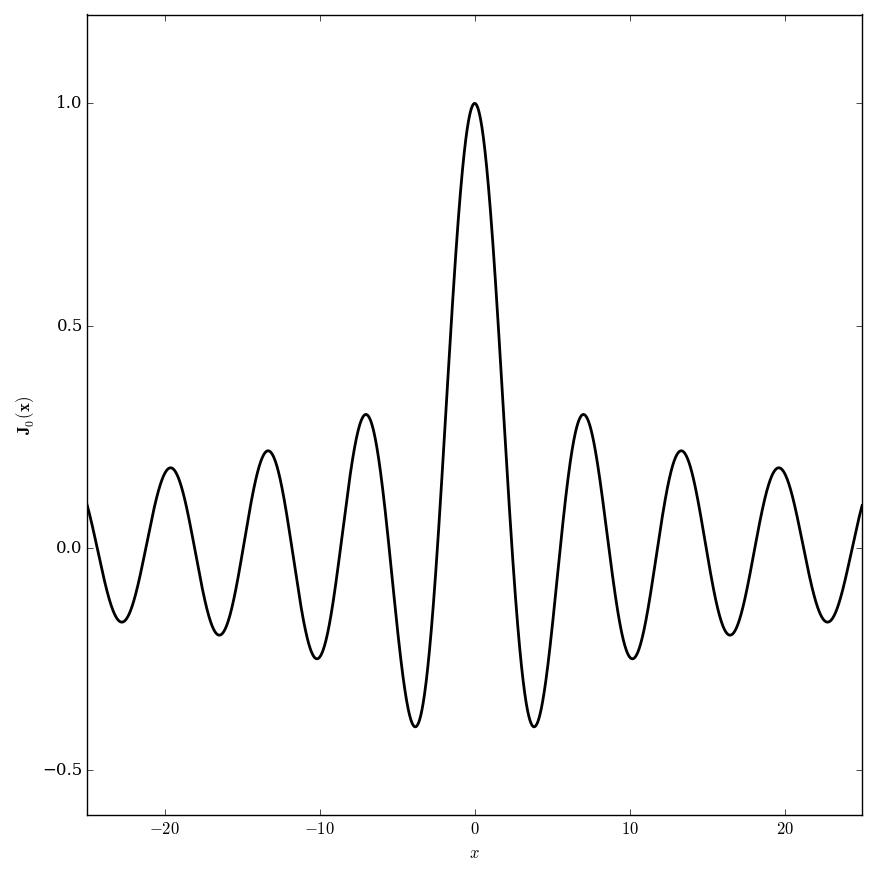
| + | File:Anger0plot.png | Graph of $\mathbf{J}_0$. | ||
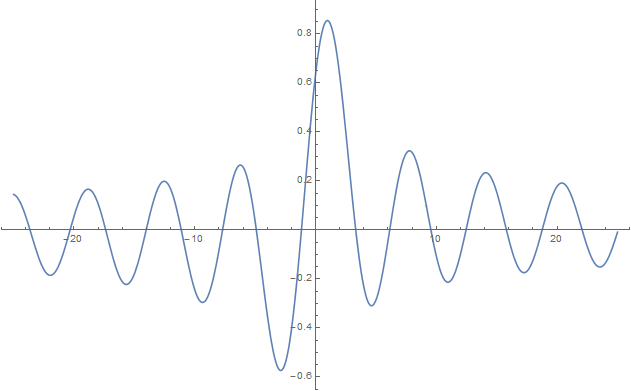
File:Angerj.png|Graph of $\mathbf{J}_{\frac{1}{2}}$. | File:Angerj.png|Graph of $\mathbf{J}_{\frac{1}{2}}$. | ||
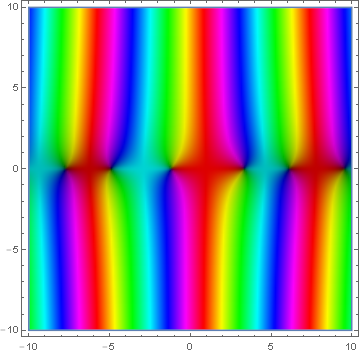
File:Domaincoloring angerj.png|[[Domain coloring]] of [[analytic continuation]] of $\mathbf{J}_{\frac{1}{2}}$. | File:Domaincoloring angerj.png|[[Domain coloring]] of [[analytic continuation]] of $\mathbf{J}_{\frac{1}{2}}$. | ||
Revision as of 16:27, 23 May 2016
The Anger function is defined by $$\mathbf{J}_{\nu}(z) = \dfrac{1}{\pi} \displaystyle\int_0^{\pi} \cos(\nu \theta - z \sin(\theta)) d\theta.$$
Graph of $\mathbf{J}_0$.
Graph of $\mathbf{J}_{\frac{1}{2}}$.
Domain coloring of analytic continuation of $\mathbf{J}_{\frac{1}{2}}$.
Contents
Properties
Theorem
The following formula holds for integer $n$: $$\mathbf{J}_n(z)=J_n(z),$$ where $\mathbf{J}_n$ denotes an Anger function and $J_n$ denotes a Bessel function of the first kind.
Proof
References
Theorem
The following formula holds: $$\sin(\nu \pi)\mathbf{E}_{\nu}(z)=\mathbf{J}_{-\nu}(z)-\cos(\nu \pi)\mathbf{J}_{\nu}(z),$$ where $\mathbf{E}_{\nu}$ denotes a Weber function and $\mathbf{J}_{\nu}$ denotes an Anger function.
Proof
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 12.3.5
Theorem
The following formula holds: $$\sin(\nu\pi)\mathbf{J}_{\nu}(z)=\cos(\nu \pi)\mathbf{E}_{\nu}(z)-\mathbf{E}_{-\nu}(z),$$ where $\mathbf{J}_{\nu}$ denotes an Anger function and $\mathbf{E}_{\nu}$ denotes a Weber function.
Proof
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 12.3.4
